题目内容
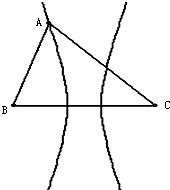如右图所示的曲线是以锐角△ABC的顶点B、C为焦点，且经过点A的双曲线，若△ABC的内角的对边分别为a，b，c，且a=4，b=6，| csinA |
| a |
| ||
| 2 |
分析：由题设知
=
=
=
，因为C为锐角，所以C=
，由余弦定理能求出c，从而得到双曲线的离心率．
| a |
| sinA |
| c | ||||
|
| c |
| sinC |
| ||
| 2 |
| π |
| 3 |
解答：解：∵
=
，
∴
=
=
=
，
因为C为锐角，所以C=
，
由余弦定理知c2=a2+b2-2abcosC=42+62-2×4×6×
=28，
c=
，
∴e=
=
=3+
．
故答案为：3+
．
| CsinA |
| a |
| ||
| 2 |
∴
| a |
| sinA |
| c | ||||
|
| c |
| sinC |
| ||
| 2 |
因为C为锐角，所以C=
| π |
| 3 |
由余弦定理知c2=a2+b2-2abcosC=42+62-2×4×6×
| 1 |
| 2 |
c=
| 2 | 7 |
∴e=
| a |
| b-c |
| 4 | |||
6-
|
| 7 |
故答案为：3+
| 7 |
点评：本题考查双曲线的性质和应用，解题时要注意三角函数的合理运用．
练习册系列答案
心算口算巧算一课一练系列答案
相关题目
的顶点
为
的双曲线，若
,且
，
(B)
(C)
(D)
的顶点B、C为焦点，且经过点A的双曲线，若
,且
，则此双曲线的离心率为（ ）
A．
如右图所示的曲线是以锐角
的顶点B、C为焦点，
,
，则此双曲线的离心率为（
）
B．
D．
如右图所示的曲线是以锐角△ABC的顶点B、C为焦点，且经过点A的双曲线，若△ABC的内角的对边分别为a，b，c，且a=4，b=6，
，则此双曲线的离心率为 ．