题目内容
过点A(3,-1)作直线l交x轴于点B,交直线l1:y=2x于点C,若|BC|=2|AB|,求直线l的方程.

解析:当k不存在时B (3,0),C(3,6).
(3,0),C(3,6).
此时|BC|=6,|AB|=1,|BC|≠2|AB|.
所以直线l的斜率存在.
所以设直线l的方程为y+1=k(x-3).
令y=0,得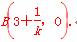
由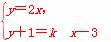 得C点横坐标xC=
得C点横坐标xC=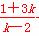 .
.
若|BC| =2|AB|,则|xB-xC|=2|xA-xB|.
=2|AB|,则|xB-xC|=2|xA-xB|.
所以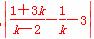 =2
=2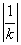 .
.
所以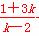 -
-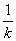 -3=
-3=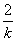 或
或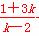 -
-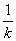 -3=-
-3=-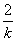 ,
,
解得k=- 或k=
或k=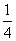 .
.
所以所求直线l的方程为:3x+2y-7=0或x-4y-7=0.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 =
= ,则点P的轨迹是( )
,则点P的轨迹是( ) 命题p:函数y=sin
命题p:函数y=sin 的图象向左平移
的图象向左平移 单位得到的曲线关于y轴对称;命题q:函数y=|3x-1|在[-1,+∞)上是增函数.则下列判断错误的是( )
单位得到的曲线关于y轴对称;命题q:函数y=|3x-1|在[-1,+∞)上是增函数.则下列判断错误的是( ) q为真命题
q为真命题
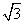 (x-1)绕点(1,0)逆时针旋转30°所得的直线方程为__________.
(x-1)绕点(1,0)逆时针旋转30°所得的直线方程为__________. 顶仰角为45°,此人沿南偏东40°方向前进10 m到D,测得塔顶A的仰角为30°,则塔高为( )
顶仰角为45°,此人沿南偏东40°方向前进10 m到D,测得塔顶A的仰角为30°,则塔高为( ) ,BC=3,AB=
,BC=3,AB= ,则∠C=( )
,则∠C=( )
 ,直线x=
,直线x= 是其图象的一条对称轴,则下面各式中符合条件的解析式为( )
是其图象的一条对称轴,则下面各式中符合条件的解析式为( )
 =
= ,则cos
,则cos 等于( )
等于( ) B.-
B.- .
.