题目内容
若cos(2π-α)=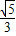 ,且α∈(-
,且α∈(-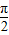 ,0),则sin(π-α)= .
,0),则sin(π-α)= .
【答案】分析:由题意求出cosα的值,利用诱导公式化简sin(π-α),结合同角三角函数的基本关系式,求出它的值即可.
解答:解:cos(2π-α)=cosα=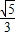 ,又α∈(-
,又α∈(-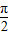 ,0),
,0),
故sin(π-α)=sinα=-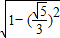 =-
=- .
.
故答案为:- .
.
点评:本题是基础题,考查同角三角函数的基本关系式,诱导公式的应用,考查计算能力,常考题型.
解答:解:cos(2π-α)=cosα=
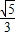 ,又α∈(-
,又α∈(-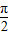 ,0),
,0),故sin(π-α)=sinα=-
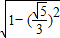 =-
=- .
.故答案为:-
 .
.点评:本题是基础题,考查同角三角函数的基本关系式,诱导公式的应用,考查计算能力,常考题型.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
已知α是第三象限角,且f(α)=
(1)化简f(α);
(2)若cos(α-
)=
,求f(α)的值.
sin(π-α)cos(2π-α)tan(-α+
| ||
|
(1)化简f(α);
(2)若cos(α-
| 3π |
| 2 |
| 1 |
| 5 |
若cos(2π-α)=
,且α∈(-
,0),则sin(π+α)=( )
2
| ||
| 3 |
| π |
| 2 |
A、-
| ||
B、-
| ||
C、
| ||
D、
|