题目内容
已知集合A={x|x2+x-6=0},函数f(x)=2x-log2x
(1)求f[f(1)]的值;
(2)若f(x)=m的解集为B,且A∩B≠ϕ,求m的值.
(1)求f[f(1)]的值;
(2)若f(x)=m的解集为B,且A∩B≠ϕ,求m的值.
考点:函数的值,交集及其运算
专题:函数的性质及应用
分析:(1)由已知得f(1)=2-log21=2,从而f[f(1)]=f(2),由此能求出结果.
(2)A={x|x2+x-6=0}={2,-3},函数f(x)的定义域为(0,+∞)由A∩B≠ϕ得2是方程的m=2x-log2x的解,由此能求出m.
(2)A={x|x2+x-6=0}={2,-3},函数f(x)的定义域为(0,+∞)由A∩B≠ϕ得2是方程的m=2x-log2x的解,由此能求出m.
解答:
解:(1)∵f(x)=2x-log2x,
∴f(1)=2-log21=2,
∴f[f(1)]=f(2)=2×2-log22=3.
(2)∵A={x|x2+x-6=0}={2,-3},f(x)=m的解集为B,且A∩B≠ϕ,
函数f(x)的定义域为(0,+∞)
∴由A∩B≠ϕ得2是方程的m=2x-log2x的解
∴m=2×2-log22=3.
∴f(1)=2-log21=2,
∴f[f(1)]=f(2)=2×2-log22=3.
(2)∵A={x|x2+x-6=0}={2,-3},f(x)=m的解集为B,且A∩B≠ϕ,
函数f(x)的定义域为(0,+∞)
∴由A∩B≠ϕ得2是方程的m=2x-log2x的解
∴m=2×2-log22=3.
点评:本题考查函数值的求法,解题时要认真审题,是基础题.

练习册系列答案
相关题目
圆x2+y2+4x+26y+b2=0与某坐标轴相切,那么b可以取得值是( )
| A、±2或±13 | B、1和2 |
| C、-1和-2 | D、-1和1 |
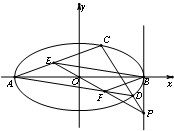 如图,在平面直角坐标系xOy中,A、B分别是椭圆:
如图,在平面直角坐标系xOy中,A、B分别是椭圆: