题目内容
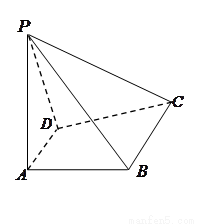
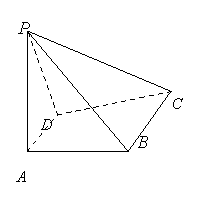
(12分)已知四棱锥![]() 中,
中,![]() 平面
平面![]() ,底面
,底面![]() 是直角梯形,
是直角梯形,![]()
![]() 为
为![]() 的重心,
的重心,![]() 为
为![]() 的中点,
的中点,![]() 在
在![]() 上,且
上,且![]() ;
;
(1)求证:![]() ;
;
(2)当二面角![]() 的正切值为多少时,
的正切值为多少时,

![]() 平面
平面![]() ;
;
(3)在(2)的条件下,求直线![]() 与平面
与平面![]() 所成角
所成角
的正弦值;
(1)连结CG并延长交PA于H,连结BH
∵G是△PAC的重心 ∴CG:GH=2:1
∵CF:FB=2:1 ∴CG:GH=CF:FB ∴FG∥BH
∵PA⊥平面ABCD ∴PA⊥AC ∴AC⊥平面PAB
 ∴ AC⊥BH ∵FG∥BH ∴FG⊥AC ------------4分
∴ AC⊥BH ∵FG∥BH ∴FG⊥AC ------------4分
(2)如图所示,以A为坐标原点建立空间直角坐标系
∵AB=AC=2且AB⊥AC ∴∠ACB=45° 在直角梯形ABCD中
∵∠BCD=90° ∴∠ACD=45°∵AC=2 ∴AD=CD=![]()
∵PA⊥平面ABCD ∴PA⊥CD ∵CD⊥AD ∴CD⊥平面PAD
∴CD⊥PD ∴∠PDA为二面角P-CD-A的平面角
∴A(0,0,0) C(![]() ,
,![]() ,0) D(0,
,0) D(0,![]() ,0) B(
,0) B(![]() ,
,![]() ,0)
,0)
设P(0,0,![]() ) ∴H(0,0,
) ∴H(0,0,![]() ) E(
) E(![]() ,
,![]() ,
,![]() )
)
∵FG⊥平面AEC ∴FG⊥AE∵FG∥BH ∴BH⊥AE
∴![]() =(
=(![]() ,
,![]() ,
,![]() )
) ![]() =(
=(![]() ,
,![]() ,
,![]() )∴
)∴![]() ∴
∴![]() ∴PA=
∴PA=![]()
∴![]() ∠PDA=2 ∴当二面角P-CD-A的正切值为2时,FG⊥平面AEC ---------------------8分
∠PDA=2 ∴当二面角P-CD-A的正切值为2时,FG⊥平面AEC ---------------------8分
(3)∵BH∥FG ∴FG与平面PBC所成的角等于BH与平面PBC所成的角
∵![]() =(
=(![]() ,
,![]() ,
,![]() )
) ![]() =(0,
=(0,![]() ,0)
,0) ![]() =(
=(![]() ,
,![]() ,
,![]() )
)
设平面PBC的法向量![]() =(x,y,z) ∴
=(x,y,z) ∴ ∴
∴![]() 令z=1 ∴
令z=1 ∴![]() =(2,0,1)
=(2,0,1)
∴![]() 设直线FG与平面PBC所成的角为
设直线FG与平面PBC所成的角为![]()
∴![]() ∴直线FG与平面PBC所成的角的正弦值为
∴直线FG与平面PBC所成的角的正弦值为![]() -----------------12分
-----------------12分

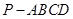 中,
中,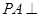 平面
平面 ,底面
,底面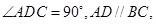
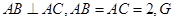 为
为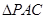 的重心,
的重心,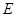 为
为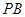 的中点,
的中点,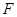 在
在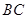 上,且
上,且 ;
;
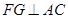 ;
; 的正切值为多少时,
的正切值为多少时,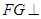 平面
平面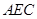 ;
;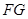 与平面
与平面 所成角
所成角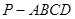 中,
中,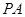 ⊥平面
⊥平面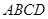 ,
,
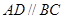 ,
,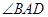
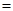 90º,
90º, .
. ⊥
⊥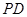 ;
;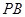 上是否存在一点
上是否存在一点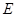 ,使
,使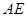 //平面
//平面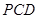 ,
,