题目内容
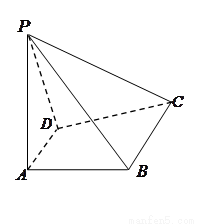
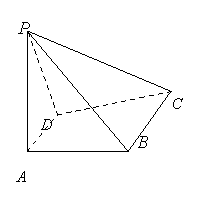
已知四棱锥![]() 中,
中,![]() 平面
平面![]() ,底面
,底面![]() 为菱形,
为菱形,![]() =60
=60![]() ,
,![]() ,
,![]() 是线段
是线段![]() 的中点.
的中点.
(1)求证:![]() ;
;
(2)求平面![]() 与平面
与平面![]() 所成锐二面角的大小;
所成锐二面角的大小;
(3)在线段![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() ∥平面PAE,并给出证明.
∥平面PAE,并给出证明.
(1)略(2) ![]() (3)线段
(3)线段![]() 上存在一点
上存在一点![]() ,使得
,使得![]() ∥平面PAE,且F是PD的中点。
∥平面PAE,且F是PD的中点。
解析:
∵四边形ABCD是![]() 的菱形,E为边BC的中点,
的菱形,E为边BC的中点,
∴AE⊥BC,AE⊥AD,又![]() 平面
平面![]() ,∴PA⊥AE,PA⊥AD,以AE、AD、AP分别为x、y、z轴建立坐标系,设AB=2,则
,∴PA⊥AE,PA⊥AD,以AE、AD、AP分别为x、y、z轴建立坐标系,设AB=2,则
![]()
![]()
![]()
![]()
![]() ,-------------1分
,-------------1分
(1)![]()
![]()
![]() -------------2分
-------------2分
∴![]() ------------------3分
------------------3分
即PE⊥AD ---------------------4分
(2)设平面PCD的法向量为![]() ,则
,则![]() ⊥
⊥![]() ,
,![]() ⊥
⊥![]() ,
,
∵![]()
![]()
![]()
∴![]()
![]()
![]()
![]()
![]() ,
,
令![]() ,则
,则![]() ,得平面PCD的一个法向量为
,得平面PCD的一个法向量为![]() ,
,
又![]() ⊥平面PAE,则
⊥平面PAE,则![]() 是平面PAE的一个法向量,设平面PAE与平面PCD所成角为
是平面PAE的一个法向量,设平面PAE与平面PCD所成角为![]() ,则
,则
![]() 所以平面
所以平面![]() 与平面
与平面![]() 所成锐二面角的大小为
所成锐二面角的大小为![]() ;------------------------8分
;------------------------8分
(3)在线段![]() 上存在一点
上存在一点![]() ,使得
,使得![]() ∥平面PAE,且F是PD的中点,
∥平面PAE,且F是PD的中点,
证明:取PA中点M,连结MF,易证四边形CFMB是平行四边形,所以CF∥EM,
又CF![]() 平面PAE,EM
平面PAE,EM![]() 平面PAE,所以
平面PAE,所以![]() ∥平面PAE.---------------------12分
∥平面PAE.---------------------12分

练习册系列答案
 作业辅导系列答案
作业辅导系列答案
相关题目
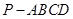 中,
中,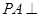 平面
平面 ,底面
,底面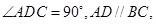
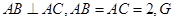 为
为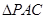 的重心,
的重心,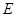 为
为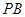 的中点,
的中点,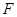 在
在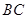 上,且
上,且 ;
;
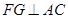 ;
; 的正切值为多少时,
的正切值为多少时,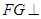 平面
平面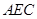 ;
;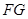 与平面
与平面 所成角
所成角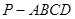 中,
中,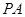 ⊥平面
⊥平面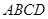 ,
,
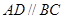 ,
,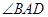
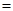 90º,
90º, .
. ⊥
⊥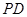 ;
;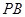 上是否存在一点
上是否存在一点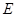 ,使
,使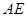 //平面
//平面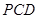 ,
,