题目内容
“k=2”是“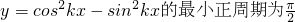 ”的
”的
- A.充分不必要条件
- B.必要不充分条件
- C.充分且必要条件
- D.既不充分也不必要条件
A
分析:把函数y=cos2kx-sin2kx利用二倍角的余弦函数公式化简,得到一个角的余弦函数,找出ω,代入周期公式T=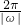 ,表示出函数的周期,把k=2代入表示出的周期中,求出周期为
,表示出函数的周期,把k=2代入表示出的周期中,求出周期为 ;把周期为
;把周期为 代入求出k=2或k=-2,进而得到“k=2”是“y=cos2kx-sin2kx的最小正周期为
代入求出k=2或k=-2,进而得到“k=2”是“y=cos2kx-sin2kx的最小正周期为 ”的充分不必要条件.
”的充分不必要条件.
解答:y=cos2kx-sin2kx=cos2kx,
∵ω=2k,
∴T=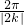 =
=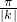 ,
,
当k=2时,T= ,
,
∴“k=2”是“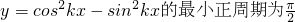 ”的充分条件;
”的充分条件;
但是T= 时,k=±2,
时,k=±2,
∴“k=2”不是“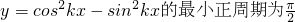 ”的必要条件,
”的必要条件,
则“k=2”是“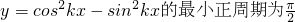 ”的充分不必要条件.
”的充分不必要条件.
故选A
点评:此题考查了必要条件、充分条件与充要条件的判断,涉及的知识有:三角函数的周期性及其求法,二倍角的余弦函数公式,其中把函数解析式利用三角函数的恒等变换化为一个角的三角函数是求函数周期的关键.
分析:把函数y=cos2kx-sin2kx利用二倍角的余弦函数公式化简,得到一个角的余弦函数,找出ω,代入周期公式T=
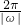 ,表示出函数的周期,把k=2代入表示出的周期中,求出周期为
,表示出函数的周期,把k=2代入表示出的周期中,求出周期为 ;把周期为
;把周期为 代入求出k=2或k=-2,进而得到“k=2”是“y=cos2kx-sin2kx的最小正周期为
代入求出k=2或k=-2,进而得到“k=2”是“y=cos2kx-sin2kx的最小正周期为 ”的充分不必要条件.
”的充分不必要条件.解答:y=cos2kx-sin2kx=cos2kx,
∵ω=2k,
∴T=
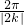 =
=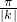 ,
,当k=2时,T=
 ,
,∴“k=2”是“
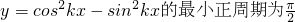 ”的充分条件;
”的充分条件;但是T=
 时,k=±2,
时,k=±2,∴“k=2”不是“
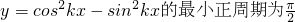 ”的必要条件,
”的必要条件,则“k=2”是“
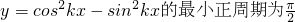 ”的充分不必要条件.
”的充分不必要条件.故选A
点评:此题考查了必要条件、充分条件与充要条件的判断,涉及的知识有:三角函数的周期性及其求法,二倍角的余弦函数公式,其中把函数解析式利用三角函数的恒等变换化为一个角的三角函数是求函数周期的关键.

练习册系列答案
相关题目