题目内容
3x2-2x在(-1，1)上恒成立． 设g(x)=3x2-2x=3(x-
)2-．∵对称轴为x=．∴g(x)<g(-1)=5．
因而要t≥g(x)在(-1，1)上恒成立．∴t≥5．即t的取值范围是[5，+∞]．
解法2：依定义f(x)=x2(1-x)+t(x+1)=-x3+x2+tx+t,f′(x)=-3x2+2x+t，
若f(x)在(-1，1)上是增函数，则在(-1，1)上恒有 f′(x)≥0，∵f′(x)的图像是开口向下的抛物线． ∴当且仅当
t≥5时，f′(x)在(-1，1)上满足f′(x)>0．即f(x)在(-1，1)上是增函数．故t的取值范围是[5，+∞]．
练习册系列答案
相关题目
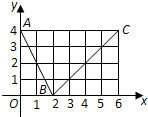如图，函数f（x）的图象是折线段ABC，其中A，B，C的坐标分别为（0，4），（2，0），（6，4），则f（f（0））=