题目内容
已知在△ABC中,边AB上的高与边AB的长相等,则 的最大值为_____.
的最大值为_____.
2
[解析]设AC=b,BC=a,AB=c,则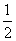 absin C=
absin C=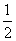 c2,即absin
c2,即absin C=c2.
C=c2.


练习册系列答案
 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
题目内容
已知在△ABC中,边AB上的高与边AB的长相等,则 的最大值为_____.
的最大值为_____.
2
[解析]设AC=b,BC=a,AB=c,则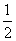 absin C=
absin C=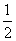 c2,即absin
c2,即absin C=c2.
C=c2.


 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案