题目内容
已知点M到两个定点A（-1，0）和B（1，0）的距离之和是定值2，则动点M的轨迹是（ ）
分析：根据A、B两点坐标可求出|AB|=2，而动点M到A、B两点距离之和为也是2，根据椭圆的定义可知点M的轨迹不是椭圆，从而得到结论．
解答：解：∵A（-1，0），B（1，0），
∴|AB|=2，
∵而动点M到A、B两点距离之和为也是2，2=2，
∴点P的轨迹不是椭圆，
∴动点M的轨迹是线段AB．
故选B．
∴|AB|=2，
∵而动点M到A、B两点距离之和为也是2，2=2，
∴点P的轨迹不是椭圆，
∴动点M的轨迹是线段AB．
故选B．
点评：椭圆的定义：平面内与两个定点A、B的距离的和等于常数（大于AB）的点的轨迹叫做椭圆，本题中条件不符合椭圆的定义，属于基础题．
练习册系列答案
相关题目
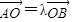，点P是C上不与A、B重合的一点，如果PA、PB的斜率都存在，问kPA•kPB是否为定值？若是，求出其值；若不是，请说明理由．