题目内容
已知动点M到两个定点F1(-3,0),F2(3,0)的距离之和为10,A、B是动点M轨迹C上的任意两点.(1)求动点M的轨迹C的方程;
(2)若原点O满足条件
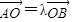 ,点P是C上不与A、B重合的一点,如果PA、PB的斜率都存在,问kPA•kPB是否为定值?若是,求出其值;若不是,请说明理由.
,点P是C上不与A、B重合的一点,如果PA、PB的斜率都存在,问kPA•kPB是否为定值?若是,求出其值;若不是,请说明理由.
【答案】分析:(1)由题意可知点M的轨迹是以F1、F2为焦点的椭圆,其中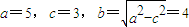 ,由此能够推导出点M的轨迹方程.
,由此能够推导出点M的轨迹方程.
(2)设A(x,y),B(-x,-y).设P(5cosθ,4sinθ),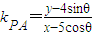 ,
,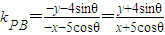 ,
,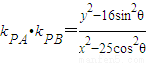 .A在椭圆上,
.A在椭圆上,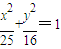 ,
,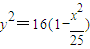 ,由此能够推导出kPA•kPB为定值-
,由此能够推导出kPA•kPB为定值-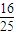 .
.
解答:解:(1)设点M的坐标为(x,y),
∵|MF1|+|MF2|=10>|F1F2|=6,
∴点M的轨迹是以F1、F2为焦点的椭圆,
其中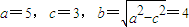 ,
,
故点M的轨迹方程为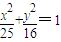 ,
,
(2)设A(x,y),当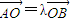 时,
时,
必有点A、B关于原点O对称,
∴B(-x,-y).
设P(5cosθ,4sinθ),
则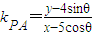 ,
,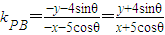 ,
,
∴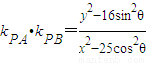 .
.
∵A在椭圆上,∴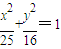 ,∴
,∴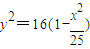 ,
,
∴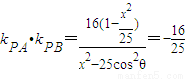 ,
,
∴kPA•kPB为定值-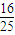 .
.
点评:本题综合考查椭圆的性质及其应用和直线与椭圆的位置关系,难度较大,解题时要认真审题,仔细解答,避免出现不必要的错误.
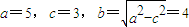 ,由此能够推导出点M的轨迹方程.
,由此能够推导出点M的轨迹方程.(2)设A(x,y),B(-x,-y).设P(5cosθ,4sinθ),
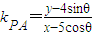 ,
,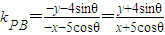 ,
,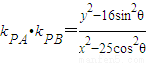 .A在椭圆上,
.A在椭圆上,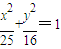 ,
,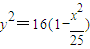 ,由此能够推导出kPA•kPB为定值-
,由此能够推导出kPA•kPB为定值-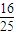 .
.解答:解:(1)设点M的坐标为(x,y),
∵|MF1|+|MF2|=10>|F1F2|=6,
∴点M的轨迹是以F1、F2为焦点的椭圆,
其中
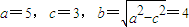 ,
,故点M的轨迹方程为
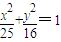 ,
,(2)设A(x,y),当
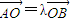 时,
时,必有点A、B关于原点O对称,
∴B(-x,-y).
设P(5cosθ,4sinθ),
则
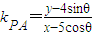 ,
,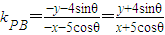 ,
,∴
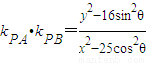 .
.∵A在椭圆上,∴
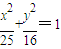 ,∴
,∴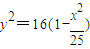 ,
,∴
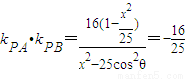 ,
,∴kPA•kPB为定值-
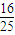 .
.点评:本题综合考查椭圆的性质及其应用和直线与椭圆的位置关系,难度较大,解题时要认真审题,仔细解答,避免出现不必要的错误.

练习册系列答案
相关题目
 的点的轨迹.
的点的轨迹.