题目内容
曲线y=e-5x+2在点（0，3）处的切线方程为 ．
考点：利用导数研究曲线上某点切线方程
专题：导数的概念及应用
分析：利用导数的几何意义求得切线的斜率，点斜式写出切线方程．
解答：
解；y′=-5e-5x，∴k=-5，
∴曲线y=e-5x+2在点（0，3）处的切线方程为y-3=-5x，即y=-5x+3．
故答案为：y=-5x+3
∴曲线y=e-5x+2在点（0，3）处的切线方程为y-3=-5x，即y=-5x+3．
故答案为：y=-5x+3
点评：本题主要考查利用导数的几何意义求曲线的切线方程，属基础题．
练习册系列答案
相关题目
掷两颗均匀的骰子，则点数之和为5的概率等于（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
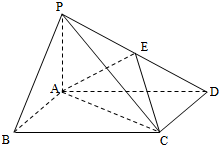如图，四棱锥P-ABCD中，底面ABCD为矩形，PA⊥平面ABCD，E为PD的中点．
如图，四棱锥P-ABCD中，AP⊥平面PCD，AD∥BC，AB=BC=