题目内容
已知函数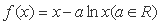 .
.
(Ⅰ)当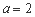 时,求曲线
时,求曲线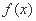 在
在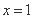 处的切线方程;
处的切线方程;
(Ⅱ)设函数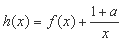 ,求函数
,求函数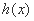 的单调区间;
的单调区间;
(Ⅲ)若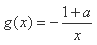 ,在
,在 上存在一点
上存在一点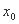 ,使得
,使得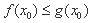 成立,求
成立,求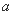 的取值范围.
的取值范围.
解:(Ⅰ)当 时,
时, ,
, ,切点
,切点 , ……1分
, ……1分
 ,
, , ……3分
, ……3分
 曲线
曲线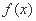 在点
在点 处的切线方程为:
处的切线方程为: ,即
,即 . ……4分
. ……4分
(Ⅱ) ,定义域为
,定义域为 ,
,
 ……5分
……5分
①当 ,即
,即 时,令
时,令 ,
,
令 ,
, ……6分
……6分
②当 ,即
,即 时,
时, 恒成立, ……7分
恒成立, ……7分
综上:当 时,
时, 在
在 上单调递减,在
上单调递减,在 上单调递增.
上单调递增.
当 时,
时, 在
在 上单调递增. ……8分
上单调递增. ……8分
(Ⅲ)由题意可知,在 上存在一点
上存在一点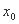 ,使得
,使得 成立,
成立,
即在 上存在一点
上存在一点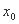 ,使得
,使得 ,
,
即函数 在
在 上的最小值
上的最小值 .… …9分
.… …9分
由第(Ⅱ)问,①当 ,即
,即 时,
时, 在
在 上单调递减,
上单调递减,
 ,
, ,
,
 ,
, ; ……10分
; ……10分
②当 ,即
,即 时,
时, 在
在 上单调递增,
上单调递增,
 ,
, ……11分
……11分
③当 ,即
,即 时,
时,

 ,
, ,
,
此时不存在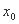 使
使 成立. ……13分
成立. ……13分
综上可得所求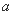 的范围是:
的范围是: 或
或 .………………14分
.………………14分

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ,则下列不等式成立的是( )
,则下列不等式成立的是( ) B.
B. C.
C. D.
D.
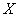 为选出的3名同学中女同学的人数,求随机变量
为选出的3名同学中女同学的人数,求随机变量 若
若 则
则 .
.  ,
, 的面积为
的面积为 ,则
,则 = .
= .  ,
, ,
, 满足|
满足| ,|
,| |=1,
|=1, •
• B.2 C.
B.2 C.