题目内容
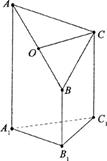
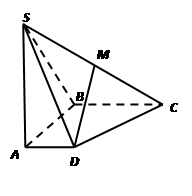
如图,在四棱锥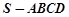 中,底面
中,底面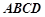 是直角梯形,
是直角梯形,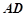 ∥
∥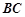 ,
,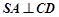 ,
,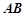 ⊥平面SAD,点
⊥平面SAD,点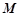 是
是 的中点,且
的中点,且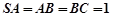 ,
,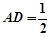 .
.
(1)求四棱锥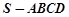 的体积;
的体积;
(2)求证: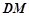 ∥平面
∥平面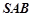 ;
;
(3)求直线 和平面
和平面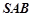 所成的角的正弦值.
所成的角的正弦值.
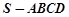 中,底面
中,底面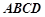 是直角梯形,
是直角梯形,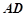 ∥
∥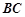 ,
,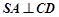 ,
,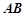 ⊥平面SAD,点
⊥平面SAD,点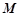 是
是 的中点,且
的中点,且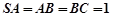 ,
,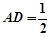 .
. 
(1)求四棱锥
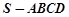 的体积;
的体积;(2)求证:
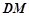 ∥平面
∥平面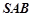 ;
;(3)求直线
 和平面
和平面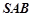 所成的角的正弦值.
所成的角的正弦值.(1)证得侧棱 底面
底面 ,体积
,体积 。
。
(2)证得 ∥
∥ 且
且
 ,
,
由四边形 是平行四边形,得到
是平行四边形,得到 ∥
∥ ,推出
,推出 ∥平面
∥平面 。
。
(3)直线 和平面
和平面 所成的角的正弦值是
所成的角的正弦值是 。
。
 底面
底面 ,体积
,体积 。
。(2)证得
 ∥
∥ 且
且
 ,
,由四边形
 是平行四边形,得到
是平行四边形,得到 ∥
∥ ,推出
,推出 ∥平面
∥平面 。
。(3)直线
 和平面
和平面 所成的角的正弦值是
所成的角的正弦值是 。
。试题分析:(1)∵
 ⊥底面
⊥底面 ,
, 底面
底面 ,
, 底面
底面
∴
 ⊥
⊥ ,
,  ⊥
⊥
∵
 ,
, 、
、 是平面
是平面 内的两条相交直线
内的两条相交直线∴侧棱
 底面
底面 2分
2分在四棱锥
 中,侧棱
中,侧棱 底面
底面 ,底面
,底面 是直角梯形,
是直角梯形, ,
, ,∴
,∴ ∥
∥ 且
且
 ,
,所以,四棱锥
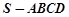 的体积是
的体积是 。
。(2)在四棱锥
 中,侧棱
中,侧棱 底面
底面 ,底面
,底面 是直角梯形,
是直角梯形, ,
,
∴
 ∥
∥ 且
且
 ,
,∴
 ∥
∥ 且
且

∴四边形
 是平行四边形
是平行四边形∴
 ∥
∥
∵
 ,
,
∴
 ∥平面
∥平面 8分
8分(3)∵侧棱
 底面
底面 ,
, 底面
底面
∴

∵
 垂直于
垂直于 ,
, 、
、 是平面
是平面 内的两条相交直线
内的两条相交直线∴
 ,垂足是点
,垂足是点
∴
 是
是 在平面
在平面 内的射影,
内的射影,
∴
 是直线
是直线 和平面
和平面 所成的角
所成的角∵在
 中,
中, ,
,
∴

∴

∴ 直线
 和平面
和平面 所成的角的正弦值是
所成的角的正弦值是 12分
12分考点:平行关系,垂直关系,体积与角的计算。
点评:中档题,立体几何问题中,平行关系、垂直关系,角、距离、面积、体积等的计算,是常见题型,基本思路是将空间问题转化成为平面问题,利用平面几何知识加以解决。要注意遵循“一作,二证,三计算”。利用“向量法”,通过建立空间直角坐标系,往往能简化解题过程。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
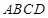 -
-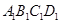 ,
,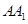 =2,
=2,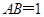 ,
,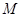 ,
,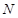 分别在
分别在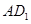 ,
,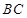 上移动,且始终保持
上移动,且始终保持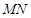 ∥平面
∥平面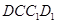 ,设
,设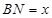 ,
,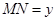 ,则函数
,则函数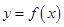 的图象大致是( )
的图象大致是( )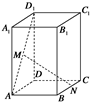
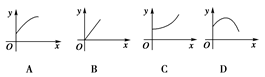


 、
、 和平面
和平面 ,若
,若 ,则“
,则“ ”是“
”是“ ”的( )
”的( ) a,则l//a ;② l//a,m//a 则 l//m; ③a丄β,l
a,则l//a ;② l//a,m//a 则 l//m; ③a丄β,l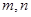 和不重合的平面
和不重合的平面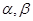 ,下列命题错误的是( )
,下列命题错误的是( ) ,则
,则
 ,则
,则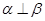
 ,则
,则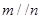
 ,则
,则
 的棱长为1,点
的棱长为1,点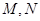 分别是
分别是 和
和 的中点
的中点

 与
与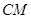 所成角的余弦值。
所成角的余弦值。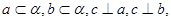 则
则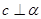 ;②。若
;②。若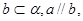 则
则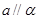 ;
;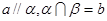 ,则
,则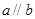 ; ④。若
; ④。若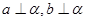 ,则
,则