题目内容

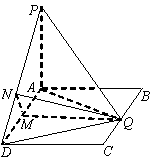
解法1:(Ⅰ)如图,连![]() ,由于PA⊥平面ABCD,则由PQ⊥QD,必有
,由于PA⊥平面ABCD,则由PQ⊥QD,必有![]() .
.
……2分
设![]() ,则
,则![]() ,
,
在![]() 中,有
中,有![]() .
.
在![]() 中,有
中,有![]() . ……4分
. ……4分
在![]() 中,有
中,有![]() .
.
即![]() ,即
,即![]() .
.
∴![]() .
.
故![]() 的取值范围为
的取值范围为![]() . ……6分
. ……6分
(Ⅱ)由(Ⅰ)知,当![]() ,
,![]() 时,边BC上存在唯一点Q(Q为BC边的中点),使PQ⊥QD. ……8分
时,边BC上存在唯一点Q(Q为BC边的中点),使PQ⊥QD. ……8分
过Q作QM∥CD交AD于M,则QM⊥AD.
∵PA⊥平面ABCD,∴PA⊥QM.∴QM⊥平面PAD.
过M作MN⊥PD于N,连结NQ,则QN⊥PD.
∴∠MNQ是二面角A-PD-Q的平面角. ……10分
在等腰直角三角形![]() 中,可求得
中,可求得![]() ,又
,又![]() ,进而
,进而![]() .
.
……12分
∴![]() .
.
故二面角A-PD-Q的余弦值为![]() . ……14分
. ……14分
解法2:(Ⅰ)以![]() 为x、y、z轴建立如图的空间直角坐标系,则
为x、y、z轴建立如图的空间直角坐标系,则
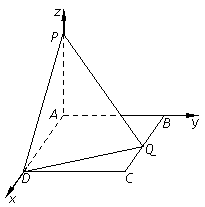 B(0,2,0),C(a,2,0),D(a,0,0),
B(0,2,0),C(a,2,0),D(a,0,0),
P(0,0,4), ……2分
设Q(t,2,0)(![]() ),则
),则 ![]() =(t,2,-4),
=(t,2,-4),
![]() =(t-a,2,0). ……4分
=(t-a,2,0). ……4分
∵PQ⊥QD,∴![]() =0.
=0.
即![]() .
.
∴![]() .
.
故![]() 的取值范围为
的取值范围为![]() . ……6分
. ……6分
(Ⅱ)由(Ⅰ)知,当![]() ,
,![]() 时,边BC上存在唯一点Q,使PQ⊥QD.
时,边BC上存在唯一点Q,使PQ⊥QD.
此时Q(2,2,0),D(4,0,0). ……8分
设![]() 是平面
是平面![]() 的法向量,
的法向量,
由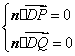 ,得
,得![]() .
.
取![]() ,则
,则![]() 是平面
是平面![]() 的一个法向量. ……10分
的一个法向量. ……10分
而![]() 是平面
是平面![]() 的一个法向量, ……12分
的一个法向量, ……12分
由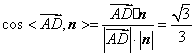 .
.
∴二面角A-PD-Q的余弦值为![]() . ……14分
. ……14分

 阶梯计算系列答案
阶梯计算系列答案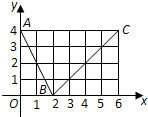 如图,函数f(x)的图象是折线段ABC,其中A,B,C的坐标分别为(0,4),(2,0),(6,4),则f(f(0))=
如图,函数f(x)的图象是折线段ABC,其中A,B,C的坐标分别为(0,4),(2,0),(6,4),则f(f(0))=