题目内容
设x1,x2是a2x2+bx+1=0的两实根;x3,x4是ax2+bx+1=0的两实根.若x3<x1<x2<x4,则实数a的取值范围是________.
a>1
分析:设f(x)=ax2+bx+1=0,方程f(x)=0为一二次函数其两实根为x1,x2(x1<x2),又x3,x4是ax2+bx+1=0的两实根,若x3<x1<x2<x4成立,即x1,x2在两其根之间,可由根的分布的相关知识将这一关系转化为不等式,解出a的范围.
解答:x1,x2是方程ax2+bx+1=0的根,∴a2x12+bx1+1=0
∴bx1=-a2x12-1,同理bx2=-a2x22-1
∴f(x1)=ax12+bx1+1=ax12-a2x12=(a-a2)x12
同理f(x2)=(a-a2)x22
要使x3<x1<x2<x4,只需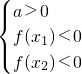 即
即  ,∴a>1
,∴a>1
或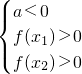 即
即 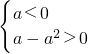 ,解集为φ
,解集为φ
故a的取值范围a>1
故答案为:a>1.
点评:本题考查一元二次方程的根的分布与系数的关系,解答的关键是对二次函数图象的特征的把握,是一道关于二次函数的综合性很强的题目.
分析:设f(x)=ax2+bx+1=0,方程f(x)=0为一二次函数其两实根为x1,x2(x1<x2),又x3,x4是ax2+bx+1=0的两实根,若x3<x1<x2<x4成立,即x1,x2在两其根之间,可由根的分布的相关知识将这一关系转化为不等式,解出a的范围.
解答:x1,x2是方程ax2+bx+1=0的根,∴a2x12+bx1+1=0
∴bx1=-a2x12-1,同理bx2=-a2x22-1
∴f(x1)=ax12+bx1+1=ax12-a2x12=(a-a2)x12
同理f(x2)=(a-a2)x22
要使x3<x1<x2<x4,只需
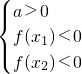 即
即  ,∴a>1
,∴a>1或
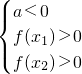 即
即 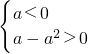 ,解集为φ
,解集为φ故a的取值范围a>1
故答案为:a>1.
点评:本题考查一元二次方程的根的分布与系数的关系,解答的关键是对二次函数图象的特征的把握,是一道关于二次函数的综合性很强的题目.

练习册系列答案
相关题目