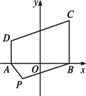
题目内容
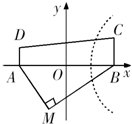 如图,某农场在M处有一堆肥料沿道路MA或MB送到大田ABCD中去,已知|MA|=6,|MB|=8,且|AD|≤|BC|,∠AMB=90°,能否在大田中确定一条界线,使位于界线一侧沿MB送肥料较近?若能,请建立适当坐标系求出这条界线方程.
如图,某农场在M处有一堆肥料沿道路MA或MB送到大田ABCD中去,已知|MA|=6,|MB|=8,且|AD|≤|BC|,∠AMB=90°,能否在大田中确定一条界线,使位于界线一侧沿MB送肥料较近?若能,请建立适当坐标系求出这条界线方程.分析:根据题意,证出界线上的任意一点P满足PA-PB=2(定值),从而得到界线为以A,B为焦点的双曲线的右支部分.在根据双曲线的基本量结合题中数据算出a=1且b=2
,算出双曲线方程,即得界线所在曲线的方程.
| 6 |
解答:解:设P为界线上的任意一点,则有PA+MA=PB+MB,即PA-PB=MB-MA=2(定值),
∴界线为以A,B为焦点的双曲线的右支
如图所示,以AB所在直线为x轴,线段AB的垂直平分线为y轴,建立直角坐标系,
设所求双曲线的标准方程为
-
=1=1(a>0,b>0)
∵2a=2,2c=AB=
=10,可得a=1,c=5,b=
=2
∴双曲线方程为x2-
=1,
∵P为以曲线右支上一点,且|AD|≤|BC|,可得x>0
即所求界线的方程为x2-
=1,(x>0).
∴界线为以A,B为焦点的双曲线的右支
如图所示,以AB所在直线为x轴,线段AB的垂直平分线为y轴,建立直角坐标系,
设所求双曲线的标准方程为
| x2 |
| a2 |
| y2 |
| b2 |
∵2a=2,2c=AB=
| 82+62 |
| c2-a2 |
| 6 |
∴双曲线方程为x2-
| y2 |
| 24 |
∵P为以曲线右支上一点,且|AD|≤|BC|,可得x>0
即所求界线的方程为x2-
| y2 |
| 24 |
点评:本题给出实际应用问题,求界线所在曲线的方程.着重考查了双曲线的定义、标准方程和圆锥曲线的实际应用等知识,属于中档题.

练习册系列答案
相关题目