题目内容
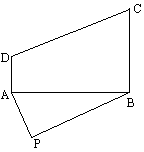
如图所示，某农场在P处有一肥堆，今要把这堆肥沿道路PA或PB送到大田ABCD中去，已知AP＝100 m，PB＝150 m，∠APB＝60°，能否在大田中确定一条界线，使位于界线一侧的点沿PA送肥较近，而另一侧的点沿PB送肥较近？如能，请确定这条界线．
答案：
解析：
解析：
|
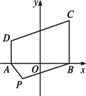
解：大田ABCD中的点分成三类：第一类设PA送肥较近，第二类沿PB送肥较近，第三类沿PA和PB送肥一样远近，第三类构成第一类、第二类点的界线，即我们所要求的轨迹，设以AB所在直线为x轴，AB的中垂线为y轴，建立直角坐标系，设M为界线所在曲线上的一点，则满足PA＋AM＝PB＋BM，于是MA－MB＝PB－PA＝50．可知M点的轨迹是以A、B为焦点的双曲线一支，其方程可求得为 |
＝1(0≤y≤60，25≤x≤35)界线为双曲线在矩形中的一段．
练习册系列答案
相关题目
，能否在大田中确定一条界线，使位于界线一侧的点沿道路PA送肥较近，而另一侧的点则沿道路PB送肥较近?如果能，请说出这条界线是一条什么曲线，并求出其方程。