Question

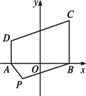
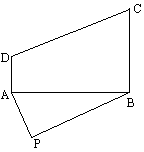
如图，某农场在P处有一堆肥，今要把这堆肥料沿道路PA或PB送到庄稼地ABCD中去，已知PA=100 m，PB=150 m，∠APB=60°.能否在田地ABCD中确定一条界线，使位于界线一侧的点，沿道路PA送肥较近；而另一侧的点，沿道路PB送肥较近?如果能，请说出这条界线是一条什么曲线，并求出其方程.

Answer 1

曲线方程为－=1(x≥25,y≥0).

解析:

设M是这种界线上的点，

则必有|MA|+|PA|=|MB|+|PB|,

即|MA|－|MB|=|PB|－|PA|=50.

∴这种界线是以A、B为焦点的双曲线靠近B点的一支.建立以AB为x轴，AB中点      O为原点的直角坐标系，则曲线为－=1,

其中a=25,c=|AB|.

∴c=25,b²=c²－a²=3750.

∴所求曲线方程为－=1(x≥25,y≥0).