题目内容
“ ”是“函数
”是“函数 的最小正周期为
的最小正周期为 ”的( ).
”的( ).
| A.充分必要条件 | B.充分不必要条件 |
| C.必要不充分条件 | D.既不充分又必要条件 |
B
解析试题分析:因为 可化为
可化为 .所以可得
.所以可得 是函数
是函数 最小正周期为
最小正周期为 的充分条件.由于函数的最小正周期为
的充分条件.由于函数的最小正周期为 ,则
,则 .所以必要性不成立.故选B.
.所以必要性不成立.故选B.
考点:1.三角函数的恒等变形.2.充要条件的知识.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
已知命题p:m<0,命题q:?x∈R,x2+mx+1>0成立,若“p∧q”为真命题,则实数m的取值范围是
| A.[-2,0] |
| B.(0,2) |
| C.(-2,0) |
| D.(-2,2) |
已知命题p:?x∈R,sin x≤1,则( ).
| A.¬p:?x0∈R,sin x0≥1 |
| B.¬p:?x∈R,sin x≥1 |
| C.¬p:?x0∈R,sin x0>1 |
| D.¬p:?x∈R,sin x>1 |
已知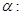 “
“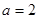 ”;
”;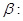 “直线
“直线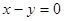 与圆
与圆 相切”.则
相切”.则 是
是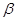 的( )
的( )
| A.充分非必要条件 | B.必要非充分条件 |
| C.充要条件 | D.既非充分也非必要条件 |
“ ”是“
”是“ ”成立的( )
”成立的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分又不必要的条件 |
已知 ,则
,则 是
是 成立的( )
成立的( )
| A.充要条件 | B.充分不必要条件 |
| C.必要不充分条件 | D.既不充分也不必要条件 |
命题“对任意x∈R,都有x2≥0”的否定为( )
| A.对任意x∈R,都有x2<0 | B.不存在x∈R,都有x2<0 |
| C.存在x0∈R,使得x02≥0 | D.存在x0∈R,使得x02<0 |
a,b,c不全为零等价为 ( )
| A.a,b,c均不为0 |
| B.a,b,c中至多有一个为0 |
| C.a,b,c中至少有一个为0 |
| D.a,b,c中至少有一个不为0 |
已知命题
 ,
, ;命题
;命题
 ,
, ,则下列命题中为真命题的是:( )
,则下列命题中为真命题的是:( )
A. |
B. |
C. |
D. |