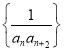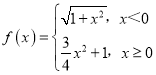题目内容
【题目】已知函数![]() ,函数
,函数![]() 的导函数
的导函数![]() ,且
,且![]() ,其中
,其中![]() 为自然对数的底数.
为自然对数的底数.
(Ⅰ)求![]() 的极值;
的极值;
(Ⅱ)若存在![]() ,使得不等式
,使得不等式![]() 成立,试求实数
成立,试求实数![]() 的取值范围;
的取值范围;
(Ⅲ)当![]() 时,对于
时,对于![]() ,求证:
,求证:![]() .
.
【答案】(Ⅰ)见解析(Ⅱ)![]() (Ⅲ)见解析
(Ⅲ)见解析
【解析】
(Ⅰ)求导,对![]() 进行分类讨论,研究单调性,求极值.
进行分类讨论,研究单调性,求极值.
(Ⅱ)先求得![]() ,分离变量,即
,分离变量,即![]() ,构造新函数,求其最大值,即可求出
,构造新函数,求其最大值,即可求出![]() 的取值范围.
的取值范围.
(Ⅲ)令![]() ,即
,即![]() ,求导研究单调性,求最小值大于0即可证得原不等式成立.
,求导研究单调性,求最小值大于0即可证得原不等式成立.
(Ⅰ)函数![]() 的定义域为
的定义域为![]() ,
,![]() .
.
当![]() 时,
时,![]() ,∴
,∴![]() 在
在![]() 上为增函数,
上为增函数,![]() 没有极值;
没有极值;
当![]() 时,令
时,令![]()
∴![]() 在
在![]() 单调递增,在
单调递增,在![]() 单调递减
单调递减
∴![]() 有极大值
有极大值![]() ,无极小值.
,无极小值.
(Ⅱ)![]() ,∴
,∴![]()
∵![]() ,∴
,∴![]()
∴![]()
∵![]() ,使得不等式
,使得不等式![]() 成立
成立
即![]()
令![]() ,
,![]()
当![]() 时,
时,![]() ,
,![]()
∴![]() ,即
,即![]() .
.
∴![]() 在
在![]() 单调递减,∴
单调递减,∴![]()
∴![]() .
.
(Ⅲ)当![]() 时,
时,![]() ,令
,令![]() ,
,
即![]()
∴![]() ,则
,则![]() 在
在![]() 上为增函数
上为增函数
∵![]() ,
,![]()
∴![]() .∵
.∵![]() 在
在![]() 上为增函数
上为增函数
∴![]() 时,
时,![]() ,
,![]() 时,
时,![]() .
.
![]() 在
在![]() 单调递减,在
单调递减,在![]() 单调递增
单调递增
∴![]()
∵![]() ∴
∴![]()
∵![]() ∴
∴![]() 单调递减,
单调递减,
∴![]()
∴![]() 即
即![]() .
.

练习册系列答案
相关题目
【题目】某学生对其亲属30人的饮食习惯进行了一次调查,并用下图所示的茎叶图表示30人的饮食指数.(说明:图中饮食指数低于70的人,饮食以蔬菜为主;饮食指数高于70的人,饮食以肉类为主)
(1)根据以上数据完成下面的2×2列联表:
主食 蔬菜 | 主食 肉类 | 总计 | |
50岁以下 | |||
50岁以上 | |||
总计 |
(2)能否在犯错误的概率不超过0.010的前提下认为“其亲属的饮食习惯与年龄有关”?并写出简要分析.
附参考公式:![]()
|
|
|
|
|
|
|
|
|
|
|
|