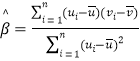题目内容
【题目】已知集合A={x|1-a≤x≤1+a}（a＞0），B={x|x2-5x+4≤0}．
（1）若“x∈A”是“x∈B”的必要不充分条件，求实数a的取值范围；
（2）对任意x∈B，不等式x2-mx+4≥0都成立，求实数m的取值范围．
【答案】（1）[3，+∞）；（2）（-∞，4].
【解析】
（1）根据“x∈A”是“x∈B”的必要不充分条件，即可得出a满足的条件．
（2）要使任意x∈B，不等式x2-mx+4≥0都成立，又B={x|x2-5x+4≤0}={x|1≤x≤4}．由x2-mx+4≥0，得
，只要
，即可得出．
解：（1）A={x|1-a≤x≤1+a}（a＞0），B={x|x2-5x+4≤0}={x|1≤x≤4}．
因为“x∈A”是“x∈B”的必要不充分条件，即BA，
所以
，或
，
所以，
，或
，
所以a≥3．
所以，实数a的取值范围是[3，+∞）．
（2）要使任意x∈B，不等式x2-mx+4≥0都成立，又B={x|x2-5x+4≤0}={x|1≤x≤4}．
由x2-mx+4≥0，得，
则只要，又
，当且仅当
，即x=2时等号成立．
实数m的取值范围（-∞，4]．
练习册系列答案
状元及第系列答案
同步奥数系列答案
相关题目
