题目内容
点P(x,y)在圆C:x2+y2-2x-2y+1=0上运动,点A(-2,2),B(-2,-2)是平面上两点,则
•
的最大值
| AP |
| BP |
7+2
| 10 |
7+2
.| 10 |
分析:利用圆的参数方程、数量积的定义及正弦函数的单调性即可求出最大值.
解答:解:由圆C:x2+y2-2x-2y+1=0化为(x-1)2+(y-1)2=1,可设x-1=cosα,y-1=sinα,(α∈[0,2π))即P(1+cosα,1+sinα),
∴
=(3+cosα,sinα-1),
=(3+cosα,3+sinα),
∴
•
=(3+cosα)2+(sinα-1)(sinα+3)=2sinα+6cosα+7=2
sin(α+φ)+7,
当sin(α+φ)=1时,
•
取得最大值2
+7.
故答案为2
+7.
∴
| AP |
| BP |
∴
| AP |
| BP |
| 10 |
当sin(α+φ)=1时,
| AP |
| BP |
| 10 |
故答案为2
| 10 |
点评:熟练掌握圆的参数方程、数量积的定义及正弦函数的单调性是解题的关键.

练习册系列答案
 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案
相关题目
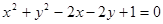 上运动,点A(-2,2),B(-2,-2)是平面上两点,则
上运动,点A(-2,2),B(-2,-2)是平面上两点,则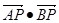 的最大值________.
的最大值________. 的参数方程为
的参数方程为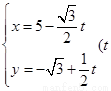 为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,圆C的极坐标方程为
为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,圆C的极坐标方程为 .
.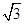 x +y的取值范围.
x +y的取值范围.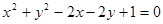 上运动,点A(-2,2),B(-2,-2)是平面上两点,则
上运动,点A(-2,2),B(-2,-2)是平面上两点,则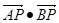 的最大值________.
的最大值________.