题目内容
(2012•江西)△ABC中,角A,B,C的对边分别为a,b,c.已知3cos(B-C)-1=6cosBcosC.
(1)求cosA;
(2)若a=3,△ABC的面积为2
,求b,c.
(1)求cosA;
(2)若a=3,△ABC的面积为2
| 2 |
分析:(1)利用两角和与差的余弦函数公式化简已知等式左边的第一项,移项合并后再利用两角和与差的余弦函数公式得出cos(B+C)的值,将cosA用三角形的内角和定理及诱导公式变形后,将cos(B+C)的值代入即可求出cosA的值;
(2)由cosA的值及A为三角形的内角,利用同角三角函数间的基本关系求出sinA的值,利用三角形的面积公式表示出三角形ABC的面积,将已知的面积及sinA的值代入,得出bc=6,记作①,再由a及cosA的值,利用余弦定理列出关于b与c的关系式,记作②,联立①②即可求出b与c的值.
(2)由cosA的值及A为三角形的内角,利用同角三角函数间的基本关系求出sinA的值,利用三角形的面积公式表示出三角形ABC的面积,将已知的面积及sinA的值代入,得出bc=6,记作①,再由a及cosA的值,利用余弦定理列出关于b与c的关系式,记作②,联立①②即可求出b与c的值.
解答:解:(1)3cos(B-C)-1=6cosBcosC,
化简得:3(cosBcosC+sinBsinC)-1=6cosBcosC,
变形得:3(cosBcosC-sinBsinC)=-1,
即cos(B+C)=-
,
则cosA=-cos(B+C)=
;
(2)∵A为三角形的内角,cosA=
,
∴sinA=
=
,
又S△ABC=2
,即
bcsinA=2
,解得:bc=6①,
又a=3,cosA=
,
∴由余弦定理a2=b2+c2-2bccosA得:b2+c2=13②,
联立①②解得:
或
.
化简得:3(cosBcosC+sinBsinC)-1=6cosBcosC,
变形得:3(cosBcosC-sinBsinC)=-1,
即cos(B+C)=-
| 1 |
| 3 |
则cosA=-cos(B+C)=
| 1 |
| 3 |
(2)∵A为三角形的内角,cosA=
| 1 |
| 3 |
∴sinA=
| 1-cos2A |
2
| ||
| 3 |
又S△ABC=2
| 2 |
| 1 |
| 2 |
| 2 |
又a=3,cosA=
| 1 |
| 3 |
∴由余弦定理a2=b2+c2-2bccosA得:b2+c2=13②,
联立①②解得:
|
|
点评:此题考查了余弦定理,三角形的面积公式,两角和与差的余弦函数公式,诱导公式,以及同角三角函数间的基本关系,熟练掌握公式及定理是解本题的关键.

练习册系列答案
相关题目

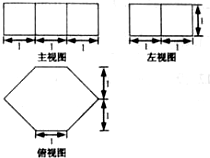 (2012•江西)若一个几何体的三视图如图所示,则此几何体的体积为( )
(2012•江西)若一个几何体的三视图如图所示,则此几何体的体积为( ) (2012•江西)在三棱柱ABC-A1B1C1中,已知AB=AC=AA1=
(2012•江西)在三棱柱ABC-A1B1C1中,已知AB=AC=AA1= (2012•江西模拟)函数f(x)=Asin(ωx+φ)的图象如图所示,其中A>0,ω>0,
(2012•江西模拟)函数f(x)=Asin(ωx+φ)的图象如图所示,其中A>0,ω>0,