题目内容
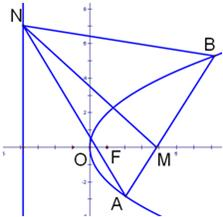 过抛物线y2=2px(p>0)的对称轴上的定点M(m,0)(m>0),作直线AB与抛物线相交于A,B两点.
过抛物线y2=2px(p>0)的对称轴上的定点M(m,0)(m>0),作直线AB与抛物线相交于A,B两点.(1)试证明A,B两点的纵坐标之积为定值;
(2)若点N是定直线l:x=-m上的任意一点,分别记直线AN,MN,BN的斜率为k1、k2、k3,
试求k1、k2、k3之间的关系,并给出证明.
分析:(1)设A(x1,y1),B(x2,y2),设直线AB的方程为:x=ty+m与y2=2px联立得y2=2px,x=ty+m,消去x得y2-2pty-2pm=0,再由韦达定理得y1•y2为定值;
(2)三条直线AN,MN,BN的斜率成等差数列,证明如下:设点N(-m,n),则直线AN的斜率为kAN=
;直线BN的斜率为kBN=
,由此能够推导出kAN+kBN=2kMN,即直线AN,MN,BN的斜率成等差数列.
(2)三条直线AN,MN,BN的斜率成等差数列,证明如下:设点N(-m,n),则直线AN的斜率为kAN=
| y1-n |
| x1+m |
| y2-n |
| x2+m |
解答:解:(1)证明:.设A(x1,y1),B(x2,y2)有y1•y2=-2pm,下证之:
设直线AB的方程为:x=ty+m与y2=2px联立得y2=2px
x=ty+m,消去x得y2-2pty-2pm=0(4分)
由韦达定理得y1•y2=-2pm,(6分)
(2)解:三条直线AN,MN,BN的斜率成等差数列,(9分)
下证之:
设点N(-m,n),则直线AN的斜率为kAN=
;
直线BN的斜率为kBN=
∴kAN+kBN=
+
=
+
=2p(
+
)=2p•
=2p•
=2p•
=2p•
=-
(13分)
又∵直线MN的斜率为kMN=
=-
(14分)
∴kAN+kBN=2kMN,即直线AN,MN,BN的斜率成等差数列. (15分)
设直线AB的方程为:x=ty+m与y2=2px联立得y2=2px
x=ty+m,消去x得y2-2pty-2pm=0(4分)
由韦达定理得y1•y2=-2pm,(6分)
(2)解:三条直线AN,MN,BN的斜率成等差数列,(9分)
下证之:
设点N(-m,n),则直线AN的斜率为kAN=
| y1-n |
| x1+m |
直线BN的斜率为kBN=
| y2-n |
| x2+m |
∴kAN+kBN=
| y1-n | ||
|
| y2-n | ||
|
=
| 2p(y1-n) |
| y12+2pm |
| 2p(y2-n) |
| y22+2pm |
=2p(
| y1-n |
| y12-y1y2 |
| y2-n |
| y22-y1y2 |
| y2(y1-n)-y1(y2-n) |
| y1y2(y1-y2) |
=2p•
| n(y1-y2) |
| y 1y2(y1-y2) |
| n |
| y1y2 |
| n |
| -2pm |
| n |
| m |
又∵直线MN的斜率为kMN=
| n-0 |
| -m-m |
| n |
| 2m |
∴kAN+kBN=2kMN,即直线AN,MN,BN的斜率成等差数列. (15分)
点评:本题考查直线和圆锥曲线的位置关系,解题时要注意公式的合理运用.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
过抛物线y2=2px(p>0)的焦点F的直线l与抛物线在第一象限的交点为A,与抛物线的准线的交点为B,点A在抛物线准线上的射影为C,若
=
,
•
=48,则抛物线的方程为( )
| AF |
| FB |
| BA |
| BC |
| A、y2=4x | ||
| B、y2=8x | ||
| C、y2=16x | ||
D、y2=4
|
过抛物线y2=2px(p>0)的焦点F作直线交抛物线于A、B两点,O为抛物线的顶点.则△ABO是一个( )
| A、等边三角形 | B、直角三角形 | C、不等边锐角三角形 | D、钝角三角形 |