Question

已知x、y为正实数,且满足关系式x²-2x+4y²=0,求x·y的最大值.

Answer 1

分析:题中有两个变量x和y,首先应选择一下因变量,将x、y表示为某一个变量(x或y或其他变量)的函数关系,实现问题的转化.同时根据题设条件确定变量的取值范围,再利用导数(或均值不等式等)求函数的最大值.

解法一:4y²=2x-x²,∵y＞0,∴y=.

∴x·y=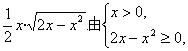解得0＜x≤2.

设f(x)=xy=(0＜x≤2).

当0＜x＜2时,f′(x)=

令f′(x)=0，得x=或x=0（舍去）.

∴.又f(2)=0,∴函数f(x)的最大值为,即x·y的最大值为.

解法二:由x²-2x+4y²=0,得(x-1)²+4y²=1(x＞0,y＞0).

设x-1=cosα,y=sinα(0＜α＜π),

∴x·y=sinα(1+cosα).

设f(α)= sinα(1+cosα),

则f′(α)= ［-sin²α+(1+cosα)·cosα］

=(2cos²α+cosα-1)=(cosα+1)(cosα-).

令f′(α)=0,得cosα=-1或cosα=.

∵0＜α＜π,∴α=,此时x=,y=.

∴f(α)_max=

即当x=,y=时,(x·y)_max=.

绿色通道:明确解决问题的策略、指向和思考方法需要抓住问题的本质,领悟真谛,巧施转化.在实现转化的过程中,关键是要注意变量的取值范围必须满足题设条件以免解题时陷于困境,功亏一篑.