题目内容
已知直线l:(3+2λ)x+(4+λ)y+2(λ-1)=0.
(1)证明不论λ为何实数,直线l恒过定点,并求出定点坐标.
(2)求直线通过的定点到直线3x-2y=1的距离.
证明:(1)由(3+2λ)x+(4+λ)y+2(λ-1)=0得:
(3x+4y-2)+λ(2x+y+2)=0,
所以有: ,
,
解得: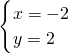 ,
,
所以直线(3+2λ)x+(4+λ)y+2(λ-1)=0通过定点(-2,2).
(2)点(-2,2)到直线3x-2y-1=0的距离
d= =
= .
.
分析:(1)将(3+2λ)x+(4+λ)y+2(λ-1)=0中的λ分离出来,化为:(3x+4y-2)+λ(2x+y+2)=0,解不等式组 即可;
即可;
(2)利用点到直线间的距离公式求之即可.
点评:本题考查直线恒过定点问题,考查点到直线间的距离公式,考查运算能力,属于中档题.
(3x+4y-2)+λ(2x+y+2)=0,
所以有:
 ,
,解得:
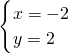 ,
,所以直线(3+2λ)x+(4+λ)y+2(λ-1)=0通过定点(-2,2).
(2)点(-2,2)到直线3x-2y-1=0的距离
d=
 =
= .
.分析:(1)将(3+2λ)x+(4+λ)y+2(λ-1)=0中的λ分离出来,化为:(3x+4y-2)+λ(2x+y+2)=0,解不等式组
 即可;
即可;(2)利用点到直线间的距离公式求之即可.
点评:本题考查直线恒过定点问题,考查点到直线间的距离公式,考查运算能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目