题目内容
已知函数
(1)当 时,试讨论函数
时,试讨论函数 的单调性;
的单调性;
(2)证明:对任意的 ,有
,有 .
.
【答案】
(1)① 时,
时, 在(0,1)是增函数,在
在(0,1)是增函数,在 是减函数;
是减函数;
② 时,
时, 在(0,1),
在(0,1), 是增函数,在
是增函数,在 是减函数;
是减函数;
③ 时,
时, 在
在 是增函数.
是增函数.
(2)见解析.
【解析】
试题分析:(1)求导数得到 ,而后根据两个驻点的大小比较,分以下三种情况讨论.
,而后根据两个驻点的大小比较,分以下三种情况讨论.
① 时,
时, 在(0,1)是增函数,在
在(0,1)是增函数,在 是减函数;
是减函数;
② 时,
时, 在(0,1),
在(0,1), 是增函数,在
是增函数,在 是减函数;
是减函数;
③ 时,
时, 在
在 是增函数.
是增函数.
(2)注意到 时,
时, 在
在 是增函数
是增函数
当 时,有
时,有 .从而得到:对任意的
.从而得到:对任意的 ,有
,有
通过构造 ,并放缩得到
,并放缩得到
利用裂项相消法求和,证得不等式。涉及数列问题,往往通过“放缩、求和”转化得到求证不等式.
试题解析:(1) 1分
1分
① 时,
时, 在(0,1)是增函数,在
在(0,1)是增函数,在 是减函数; 3分
是减函数; 3分
② 时,
时, 在(0,1),
在(0,1), 是增函数,在
是增函数,在 是减函数; 5分
是减函数; 5分
③ 时,
时, 在
在 是增函数. 6分
是增函数. 6分
(2)由(1)知 时,
时, 在
在 是增函数
是增函数
当 时,
时, .
.
对任意的 ,有
,有
 8分
8分
 10分
10分
所以
 12分
12分
考点:应用导数研究函数的单调性,应用导数证明不等式,“裂项相消法”求和.

练习册系列答案
相关题目
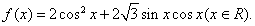
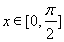
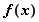

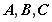
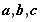
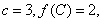
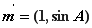
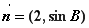
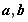

 时,求函数的最大值和最小值;
时,求函数的最大值和最小值; 的取值范围,使
的取值范围,使 在区间
在区间 上是单调减函数
上是单调减函数 .(
.( ).
). 时,求函数
时,求函数 的极值;
的极值; (2)若对
(2)若对 ,有成立,求实数
,有成立,求实数 的取值范围.
的取值范围.
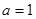 时,求
时,求 的极小值;
的极小值; ,求
,求 的最大值
的最大值 .
.