题目内容
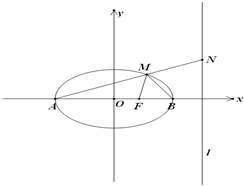
 已知定点M(0,-1),点N是⊙F:x2+(y-1)2=8(F为圆心)上的动点,线段MN的垂直平分线交NF于点G,记点G的轨迹为曲线E.
已知定点M(0,-1),点N是⊙F:x2+(y-1)2=8(F为圆心)上的动点,线段MN的垂直平分线交NF于点G,记点G的轨迹为曲线E.(Ⅰ)求曲线E的方程;
(Ⅱ)若直线l:y=kx+1与曲线E相交于A、B两个不同点,以AB为直径的圆经过坐标原点,求直线l方程.
考点:直线与圆锥曲线的综合问题
专题:综合题,圆锥曲线的定义、性质与方程
分析:(Ⅰ)由题意得|GM|=|GN|,|GM|+|GF|=|GN|+|GF|=r=2
>|AF|=2,根据椭圆的定义可求得动点G的轨迹E的方程;
(II)直线l:y=kx+1与曲线E联立得(2+k2)x2+2kx-1=0,设A(x1,y1)B(x2,y2)因为以AB为直径的圆经过原点O,得出x1x2+y1y2=0.由根与系数的关系得x1x2+y1y2=(1+k2)x1x2+k(x1+x2)+1=0解得k,即可求出直线的方程.
| 2 |
(II)直线l:y=kx+1与曲线E联立得(2+k2)x2+2kx-1=0,设A(x1,y1)B(x2,y2)因为以AB为直径的圆经过原点O,得出x1x2+y1y2=0.由根与系数的关系得x1x2+y1y2=(1+k2)x1x2+k(x1+x2)+1=0解得k,即可求出直线的方程.
解答:
解:(Ⅰ)由题意得|GM|=|GN|,
∴|GM|+|GF|=|GN|+|GF|=r=2
>|AF|=2
∴G点轨迹是以M、F为焦点的椭圆.
2a=2
,a=
,a2-b2=c2=1,故b2=1,
∴点G的轨迹方程为
+x2=1;
(Ⅱ)直线l:y=kx+1与曲线E联立得(2+k2)x2+2kx-1=0
设A(x1,y1)B(x2,y2),则x1x2=-
,x1+x2=-
∵以AB为直径的圆经过原点O,∴OA⊥OB,
∴x1x2+y1y2=0
∴(1+k2)x1x2+k(x1+x2)+1=
=0,
∴k=±
,
∴直线l方程为y=±
x+1.
∴|GM|+|GF|=|GN|+|GF|=r=2
| 2 |
∴G点轨迹是以M、F为焦点的椭圆.
2a=2
| 2 |
| 2 |
∴点G的轨迹方程为
| y2 |
| 2 |
(Ⅱ)直线l:y=kx+1与曲线E联立得(2+k2)x2+2kx-1=0
设A(x1,y1)B(x2,y2),则x1x2=-
| 1 |
| k2+2 |
| 2k |
| k2+2 |
∵以AB为直径的圆经过原点O,∴OA⊥OB,
∴x1x2+y1y2=0
∴(1+k2)x1x2+k(x1+x2)+1=
| 1-2k2 |
| k2+2 |
∴k=±
| ||
| 2 |
∴直线l方程为y=±
| ||
| 2 |
点评:本题考查椭圆的定义和几何性质,解决这种求椭圆的方程问题关键是熟悉椭圆中a,b,c之间的关系,解决求直线方程问题关键是把垂直问题转化为向量垂直再结合者根与系数的关系列方程解方程即可,此知识点是高考考查的重点.

练习册系列答案
相关题目
 一束光线从点F1(-1,0)出发,经直线l:x+2y+6=0上一点M反射后,恰好穿过点F2(1,0).
一束光线从点F1(-1,0)出发,经直线l:x+2y+6=0上一点M反射后,恰好穿过点F2(1,0).