题目内容
9.下列选项中为函数f(x)=cos(2x-$\frac{π}{6}$)sin2x-$\frac{1}{4}$的对称中心为( )| A. | $(\frac{π}{12},0)$ | B. | $(\frac{π}{3},-\frac{1}{4})$ | C. | $(\frac{π}{3},0)$ | D. | $(\frac{7π}{24},0)$ |
分析 利用三角恒等变换,化简函数的解析式,再利用正弦函数的图象的对称性,求得函数的对称中心.
解答 解:函数f(x)=cos(2x-$\frac{π}{6}$)sin2x-$\frac{1}{4}$=[$\frac{\sqrt{3}}{2}$cos2x+$\frac{1}{2}$sin2x]sin2x-$\frac{1}{4}$=$\frac{\sqrt{3}}{2}$sin2xcos2x+$\frac{1}{2}$sin22x-$\frac{1}{4}$
$\frac{\sqrt{3}}{4}$sin4x+$\frac{1}{2}$•$\frac{1-cos4x}{2}$-$\frac{1}{4}$=$\frac{1}{2}$sin(4x-$\frac{π}{6}$),
令4x-$\frac{π}{6}$=kπ,求得x=$\frac{kπ}{4}$+$\frac{π}{24}$,可得函数的对称中心为($\frac{kπ}{4}$+$\frac{π}{24}$,0),k∈Z,
当k=1时,函数的对称中心为$(\frac{7π}{24},0)$.
故选:D.
点评 本题主要考查三角恒等变换,正弦函数的图象的对称性,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
20.已知集合A={1,2},B={(x,y)|x∈A,y∈A,x-y∈A},则B的子集共有( )
| A. | 2个 | B. | 4个 | C. | 6个 | D. | 8个 |
4.已知矩形ABCD中,AB=4$\sqrt{3}$,BC=4,M,N分别是边BC,CD上的点,且MN=2,则$\overrightarrow{AM}•\overrightarrow{AN}$的最小值是( )
| A. | 12 | B. | 24 | C. | 36 | D. | 48 |
1.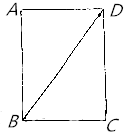 如图.矩形ABCD中,4BC=3AB,E为矩形ABCD所在平面内一点,若$\overrightarrow{CE}$=λ$\overrightarrow{BD}$且$\overrightarrow{AE}$⊥$\overrightarrow{CE}$,则λ=( )
如图.矩形ABCD中,4BC=3AB,E为矩形ABCD所在平面内一点,若$\overrightarrow{CE}$=λ$\overrightarrow{BD}$且$\overrightarrow{AE}$⊥$\overrightarrow{CE}$,则λ=( )
 如图.矩形ABCD中,4BC=3AB,E为矩形ABCD所在平面内一点,若$\overrightarrow{CE}$=λ$\overrightarrow{BD}$且$\overrightarrow{AE}$⊥$\overrightarrow{CE}$,则λ=( )
如图.矩形ABCD中,4BC=3AB,E为矩形ABCD所在平面内一点,若$\overrightarrow{CE}$=λ$\overrightarrow{BD}$且$\overrightarrow{AE}$⊥$\overrightarrow{CE}$,则λ=( )| A. | $\frac{1}{5}$ | B. | $\frac{7}{25}$ | C. | $\frac{8}{25}$ | D. | $\frac{1}{3}$ |