题目内容
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),将曲线
为参数),将曲线![]() 上各点纵坐标伸长到原来的2倍(横坐标不变)得到曲线
上各点纵坐标伸长到原来的2倍(横坐标不变)得到曲线![]() ,以坐标原点
,以坐标原点![]() 为极点,
为极点,![]() 轴正半轴为极轴,建立极坐标系,直线
轴正半轴为极轴,建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出![]() 的极坐标方程与直线
的极坐标方程与直线![]() 的直角坐标方程;
的直角坐标方程;
(2)曲线![]() 上是否存在不同的两点
上是否存在不同的两点![]() ,
,![]() (以上两点坐标均为极坐标,
(以上两点坐标均为极坐标,![]() ,
,![]() ),使点
),使点![]() 、
、![]() 到
到![]() 的距离都为3?若存在,求
的距离都为3?若存在,求![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【答案】(1)![]() ,
,![]() (2)存在,
(2)存在,![]()
【解析】
(1)先求得曲线![]() 的普通方程,利用伸缩变换的知识求得曲线
的普通方程,利用伸缩变换的知识求得曲线![]() 的直角坐标方程,再转化为极坐标方程.根据极坐标和直角坐标转化公式,求得直线
的直角坐标方程,再转化为极坐标方程.根据极坐标和直角坐标转化公式,求得直线![]() 的直角坐标方程.
的直角坐标方程.
(2)求得曲线![]() 的圆心和半径,计算出圆心
的圆心和半径,计算出圆心![]() 到直线
到直线![]() 的距离,结合图像判断出存在
的距离,结合图像判断出存在![]() 符合题意,并求得
符合题意,并求得![]() 的值.
的值.
(1)曲线![]() 的普通方程为
的普通方程为![]() ,纵坐标伸长到原来的2倍
,纵坐标伸长到原来的2倍 ,得到曲线
,得到曲线![]() 的直角坐标方程为
的直角坐标方程为![]() ,其极坐标方程为
,其极坐标方程为![]() ,
,
直线![]() 的直角坐标方程为
的直角坐标方程为![]() .
.
(2)曲线![]() 是以
是以![]() 为圆心,
为圆心,![]() 为半径的圆,
为半径的圆,
圆心![]() 到直线
到直线![]() 的距离
的距离![]() .
.
∴由图像可知,存在这样的点![]() ,
,![]() ,则
,则![]() ,且点
,且点![]() 到直线
到直线![]() 的距离
的距离![]() ,
,
∴![]() ,∴
,∴![]() .
.


【题目】某大型科学竞技真人秀节目挑选选手的方式为:不但要对选手的空间感知、照相式记忆能力进行考核,而且要让选手经过名校最权威的脑力测试,120分以上才有机会入围.某重点高校准备调查脑力测试成绩是否与性别有关,在该高校随机抽取男、女学生各100名,然后对这200名学生进行脑力测试.规定:分数不小于120分为“入围学生”,分数小于120分为“未入围学生”.已知男生入围24人,女生未入围80人.
(1)根据题意,填写下面的2×2列联表,并根据列联表判断是否有95%以上的把握认为脑力测试后是否为“入围学生”与性别有关;
性别 | 入围人数 | 未入围人数 | 总计 |
男生 | |||
女生 | |||
总计 |
(2)用分层抽样的方法从“入围学生”中随机抽取11名学生,求这11名学生中男、女生人数;若抽取的女生的脑力测试分数各不相同(每个人的分数都是整数),分别求这11名学生中女生测试分数平均分的最小值.
|
|
|
|
|
|
|
|
|
|
附: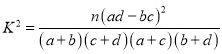 ,其中
,其中![]() .
.
【题目】某校举行了全体学生的一分钟跳绳比赛,为了了解学生的体质,随机抽取了100名学生,其跳绳个数的频数分布表如下:
一分钟跳绳个数 |
|
|
|
|
|
|
|
频数 | 6 | 12 | 18 | 30 | 16 | 10 | 8 |
(1)若将抽取的100名学生一分钟跳绳个数作为一个样本,请将这100名学生一分钟跳绳个数的频率分布直方图补充完整(只画图,不需要写出计算过程);
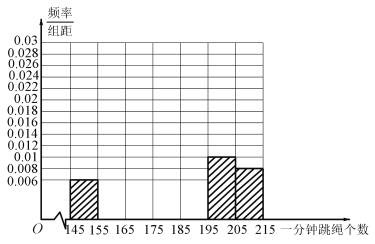
(2)若该校共有3000名学生,所有学生的一分钟跳绳个数X近似服从正态分布![]() ,其中
,其中![]() 为样本平均数的估计值(同一组中的数据用该组区间的中点值为代表).利用所得正态分布模型,解决以下问题:
为样本平均数的估计值(同一组中的数据用该组区间的中点值为代表).利用所得正态分布模型,解决以下问题:
①估计该校一分钟跳绳个数超过165个的人数(结果四舍五入到整数);
②若在该校所有学生中任意抽取4人,设一分钟跳绳个数超过180个的人数为![]() ,求随机变量
,求随机变量![]() 的分布列、期望与方差./span>
的分布列、期望与方差./span>
附:若随机变量Z服从正态分布![]() ,则
,则![]() ,
,![]() ,
,![]() .
.