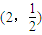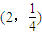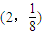题目内容
(18)已知函数f(x)=Asin![]() 且y=f(x)的最大值为2,其图象相邻两对称轴间的距离为2,并过点(1,2).
且y=f(x)的最大值为2,其图象相邻两对称轴间的距离为2,并过点(1,2).
(Ⅰ)求![]() ;
;
(Ⅱ)计算f(1)+f(2)+…+f(2008).
(Ⅰ)y=Asin2(ωx+φ)=![]() cos(2ωx+2φ).
cos(2ωx+2φ).
∵y=f(x)的最大值为2,A>0,
∴![]() =2,
=2,![]() =2.
=2.
又∵其图象相邻两对称轴间的距离为2,ω>0,
∴![]() =2,ω=
=2,ω=![]() .
.
∴f(x)=![]() cos(
cos(![]() +2φ)=1-cos(
+2φ)=1-cos(![]() +2φ).
+2φ).
∵y=f(x)过(1,2)点,
∴cos(![]() +2φ)=-1.
+2φ)=-1.
∴![]() +2φ=2kπ+π,k∈Z,
+2φ=2kπ+π,k∈Z,
∴2φ=2kπ+![]() ,k∈Z,
,k∈Z,
∴φ=kπ+![]() ,k∈Z.
,k∈Z.
又∵0<φ<![]() ,
,
∴φ=![]() .
.
(Ⅱ)解法一:∵φ=![]() ,
,
∴y=1-cos(![]() x+
x+![]() )=1+sin
)=1+sin![]() x.
x.
∴f(1)+f(2)+f(3)+f(4)=2+1+0+1=4.
又∵y=f(x)的周期为4,2008=4×502.
∴f(1)+f(2)+…+f(2008)=4×502=2008.
解法二:∵f(x)=2sin2(![]() x+φ)
x+φ)
∴f(1)+f(3)=2sin2(![]() +φ)+2sin2(
+φ)+2sin2(![]() π+φ)=2,
π+φ)=2,
f(2)+f(4)=2sin2(![]() +φ)+2sin2(π+φ)=2,
+φ)+2sin2(π+φ)=2,
∴f(1)+f(2)+f(3)+f(4)=4.
又y=f(x)的周期为4,2008=4×502.
∴f(1)+f(2)+…+f(2008)=4×502=2008.

练习册系列答案
相关题目
(上海春卷18)已知函数f(x)=
的图象关于点P对称,则点P的坐标是( )
| 1 |
| 4-2x |
A、(2,
| ||
B、(2,
| ||
C、(2,
| ||
| D、(0,0) |
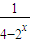 的图象关于点P对称,则点P的坐标是( )
的图象关于点P对称,则点P的坐标是( )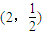
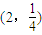
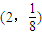
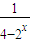 的图象关于点P对称,则点P的坐标是( )
的图象关于点P对称,则点P的坐标是( )