题目内容

在直角坐标系xoy中，点P到两点(-
3
，0)，(
3
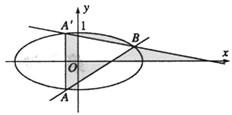
，0)的距离之和等于4，设点P的轨迹为C，直线y=kx+2与C交于不同的两点A，B．
（1）写出C的方程；
（2）求证：-1＜
OA
•
OB
＜
13
4
．
（1）由题意可得，点P是以P(-
3
，0)，(
3
，0)为焦点的椭圆，且2a=4
∴a=2，c=
3
，b2=a2-c2=1
曲线C的方程为
x2
4
+y2=1
（2）联立方程
y=kx+2
x2
4
+y2=1
可得（1+4k2）x2+16kx+12=0
由△=4k2-3＞0可得k2＞
3
4

设A（x1，y1）B（x2，y2） x1+x2=-
16k
1+4k2
x1x2=
12
1+4k2

∵
OA
•
OB
=x1x2+y1y2=（1+k2）x1x2+2k（x1+x2）+4
=(1+k2)•
12
1+4k2
+2k•
-16k
1+4k2
+4=
16-4k2
1+4k2

令y=
16-4k2
1+4k2
则可得k2=
16-y
4(y+1)
＞
3
4

∴-1＜y＜
13
4
即-1＜
OA
•
OB
＜
13
4
练习册系列答案
相关题目
如图，椭圆C：
x2
a2
+
y2
b2
=1(a＞b＞0)经过点（0，1），离心率e=
3
2
．
（l）求椭圆C的方程；
（2）设直线x=my+1与椭圆C交于A，B两点，点A关于x轴的对称点为A′（A′与B不重合），则直线A′B与x轴是否交于一个定点？若是，请写出定点坐标，并证明你的结论；若不是，请说明理由．
若方程
x2
25-k
+
y2
k-9
=1表示椭圆，则k的取值范围是（　　）
A．（9，17）B．（9，25）C．（9，17）∪（17，25）D．（-∞，9）∪（25，+∞）
如图，F是中心在原点、焦点在x轴上的椭圆C的右焦点，\直线l：x=4是椭圆C的右准线，F到直线l的距离等于3．
（1）求椭圆C的方程；
（2）点P是椭圆C上动点，PM⊥l，垂足为M．是否存在点P，使得△FPM为等腰三角形？若存在，求出点P的坐标；若不存在，说明理由．
已知椭圆过点（3，0）且离心率为
6
3
，则椭圆标准方程为______．
若方程
x2
m-1
+
y2
3-m
=1表示焦点在y轴上的椭圆，则实数m的取值范围为______．
已知椭圆
x2
2
+y2=1的左右焦点分别为F1，F2，若过点P（0，-2）及F1的直线交椭圆于A，B两点，求△ABF2的面积．
请阅读以下材料，然后解决问题：
①设椭圆的长半轴长为m短半轴长为b，则椭圆的面积为πab
②我们把由半椭圆C1：
y2
b2
+
x2
c2
=1（x≤0）与半椭圆C2：
x2
a2
+
y2
b2
=1（x≥0）合成的曲线称作“果圆”，其中a2=b2+c2，a＞0，b＞c＞0
如图，设点F0，F1，F2是相应椭圆的焦点，A1，A2和B1，B2是“果圆”与x，y轴的交点，若△F0F1F2是边长为1的等边三角形，则上述“果圆”的面积为：______．
已知椭圆
x2
a2
+
y2
b2
=1（a＞b＞0）的左右焦点分别为F1，F2，P是椭圆上的一点，且|PF1|，|F1F2|，|PF2|成等比数列，则椭圆的离心率的取值范围为（　　）
A．[
1
2
，
2
2
]		B．[
5
-1，
1
2
]		C．[
2
-1，
1
2
]		D．[
5
5
，
1
2
]

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网