题目内容
19.已知函数f(x)=(sin$\frac{x}{2}$+cos$\frac{x}{2}$)2-2$\sqrt{3}$cos2$\frac{x}{2}$+$\sqrt{3}$.(1)求f(x)的单调区间;
(2)求f(x)在[0,π]上的值域.
分析 (1)利用二倍角和辅助角公式基本公式将函数化为y=Asin(ωx+φ)的形式,将内层函数看作整体,放到正弦函数的区间上,解不等式得函数的单调递增(递减)区间;
(2)x∈[0,π]时,求出内层函数的取值范围,结合三角函数的图象和性质,求出f(x)的最大和最小值,即得到f(x)的值域.
解答 解:(1)函数f(x)=(sin$\frac{x}{2}$+cos$\frac{x}{2}$)2-2$\sqrt{3}$cos2$\frac{x}{2}$+$\sqrt{3}$.
化简可得:f(x)=1+sinx-$\sqrt{3}-\sqrt{3}$cosx+$\sqrt{3}$=sinx-$\sqrt{3}$cosx+1=2sin(x-$\frac{π}{3}$)+1,
由$-\frac{π}{2}+2kπ≤x-\frac{π}{3}≤\frac{π}{2}+2kπ$得$2kπ-\frac{π}{6}$≤x≤$\frac{5π}{6}+2kπ$,
∴f(x)的单调增区间为[$2kπ-\frac{π}{6}$,$\frac{5π}{6}+2kπ$],k∈Z.
由$\frac{π}{2}+2kπ≤x-\frac{π}{3}≤\frac{3π}{2}+2kπ$得$\frac{5π}{6}+2kπ$≤x≤$\frac{11π}{6}$+2kπ,
∴f(x)的单调减区间为[$\frac{5π}{6}+2kπ$,$\frac{11π}{6}+2kπ$],k∈Z.
(2)由(1)可知f(x)=2sin(x-$\frac{π}{3}$)+1,
∵x∈[0,π]上,
∴x-$\frac{π}{3}$∈[$-\frac{π}{3}$,$\frac{2π}{3}$],
当x-$\frac{π}{3}$=$-\frac{π}{3}$时,函数f(x)取得最小值为$-\frac{\sqrt{3}}{2}×2+1$=1$-\sqrt{3}$.
当x-$\frac{π}{3}$=$\frac{π}{2}$时,函数f(x)取得最大值为1×2+1=3.
故得函数f(x)在[0,π]上的值域为[$1-\sqrt{3}$,3].
点评 本题主要考查对三角函数的化简能力和三角函数的图象和性质的运用,利用三角函数公式将函数进行化简是解决本题的关键.属于中档题

 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案| A. | 170石 | B. | 180石 | C. | 190石 | D. | 200石 |
| A. | $\frac{1}{n}>\frac{1}{m}$ | B. | |n|>|m| | C. | $\frac{n}{m}+\frac{m}{n}>2$ | D. | m+n>mn |
| 对篮球运动不感兴趣 | 对篮球运动感兴趣 | 总计 | |
| 男生 | 20 | 50 | 70 |
| 女生 | 10 | 40 | 50 |
| 总计 | 30 | 90 | 120 |
(2)采用分层抽样的方法从“对篮球运动不感兴趣”的学生里抽取一个6人的样本,其中男生和女生个多少人?从6人中随机选取3人做进一步的调查,求选取的3人中至少有1名女生的概率
参考公式:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d
参考数据:
| P(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.706 | 3.841 | 5.024 | 5.635 | 7.879 | 10.828 |
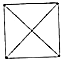
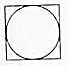
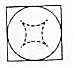
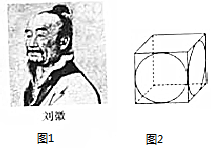 我国古代数学家刘徽(如图1)在学术研究中,不迷信古人,坚持实事求是,他对《九章算术》中“开立圆术”给出的公式产生质疑,为了证实自己的猜测,他引入了一种新的几何体“牟盒方盖”:一正方体相邻的两个侧面为底座两次内切圆柱切割,然后剔除外部,剩下的内核部分(如图2).如果“牟盒方盖”的主视图和左视图都是圆,则其俯视图形状为下列几幅图中的( )
我国古代数学家刘徽(如图1)在学术研究中,不迷信古人,坚持实事求是,他对《九章算术》中“开立圆术”给出的公式产生质疑,为了证实自己的猜测,他引入了一种新的几何体“牟盒方盖”:一正方体相邻的两个侧面为底座两次内切圆柱切割,然后剔除外部,剩下的内核部分(如图2).如果“牟盒方盖”的主视图和左视图都是圆,则其俯视图形状为下列几幅图中的( )
 如图,设椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{x}^{2}}{{b}^{2}}$=1(a>b>0)的左右焦点分别为F1,F2,离心率为e=$\frac{\sqrt{2}}{2}$,右准线L上两动点M,N,F2为△F1MN的垂心.
如图,设椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{x}^{2}}{{b}^{2}}$=1(a>b>0)的左右焦点分别为F1,F2,离心率为e=$\frac{\sqrt{2}}{2}$,右准线L上两动点M,N,F2为△F1MN的垂心.