题目内容
(文) 已知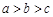 且
且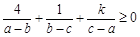 恒成立,则k的最大值是( )
恒成立,则k的最大值是( )
| A.4 | B.8 | C.9 | D.25 |
C
解析试题分析:因为,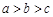 ,所以令a-b=m>0,b-c=n>0,则c-a=-(m+n)。
,所以令a-b=m>0,b-c=n>0,则c-a=-(m+n)。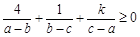 恒成立,即
恒成立,即 恒成立。
恒成立。
所以, ,
, ,
,
而 ,所以5+4≥k,k≤9,k的最大值是,选C。
,所以5+4≥k,k≤9,k的最大值是,选C。
考点:本题主要考查均值定理的应用,不等式恒成立问题。
点评:中档题,不等式恒成立问题,往往利用分离参数法,转化成求函数的最值问题。

练习册系列答案
相关题目
函数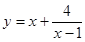
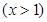 的最小值是( )
的最小值是( )
| A.3 | B.4 | C.5 | D.6 |
设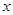 、
、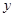 为正数,则
为正数,则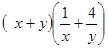 的最小值为( )
的最小值为( )
A.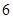 | B.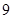 | C.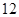 | D.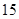 |
已知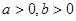 ,且函数
,且函数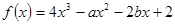 在
在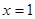 处有极值,则
处有极值,则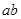 的最大值等于( )
的最大值等于( )
A.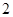 | B.3 | C.6 | D.9 |
设x>0,y>0,x+y+xy=2,则x+y的最小值是( )
A.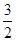 | B.1 + 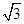 | C.2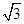 -2 -2 | D.2-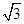 |
点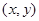 在直线
在直线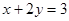 上移动,则
上移动,则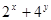 的最小值为( )
的最小值为( )
A.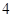 | B.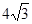 | C. | D. |
若正数 满足
满足 ,则
,则 的最小值是( )
的最小值是( )
| A.6 | B.5 | C. | D. |
设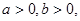 则以下不等式中不恒成立的是
则以下不等式中不恒成立的是
A.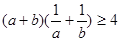 | B.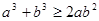 |
C. | D.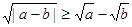 |
 、
、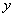 满足
满足 ,则
,则 的最小值为( )
的最小值为( ) 1
1