题目内容
设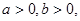 则以下不等式中不恒成立的是
则以下不等式中不恒成立的是
A.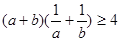 | B.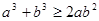 |
C. | D.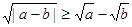 |
D
解析试题分析:对于A: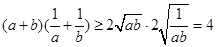 .对于B:
.对于B: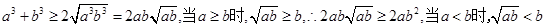 ,
,
显然不等式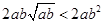 ,所以
,所以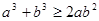 不恒成立.
不恒成立.
对于C: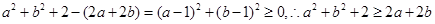 .
.
对于D:当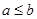 时,显然
时,显然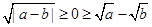 ;当
;当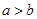 时,
时,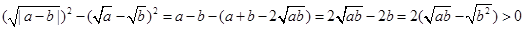
所以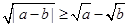 恒成立.
恒成立.
考点:基本不等式的性质,作差法判断值的大小.
点评:掌握基本不等式的成立的条件:a>0,b>0,则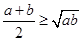 ;直接比较两个数大小不易比较时,可考虑作差法比较.
;直接比较两个数大小不易比较时,可考虑作差法比较.

练习册系列答案
相关题目
(文) 已知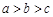 且
且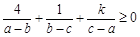 恒成立,则k的最大值是( )
恒成立,则k的最大值是( )
| A.4 | B.8 | C.9 | D.25 |
设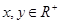 且
且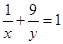 ,则
,则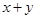 的最小值为( )
的最小值为( )
| A.12 | B.15 | C.16 | D.-16 |
设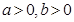 若
若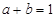 ,则
,则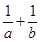 最小值为
最小值为
| A.8 | B.4 | C.1 | D.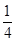 |
.已知实数 ,则M的最小值为( )
,则M的最小值为( )
A. | B.2 | C.4 | D.1 |
已知a>0,b>0, ,则
,则 的取值范围是( )
的取值范围是( )
| A.( 2,+∞) | B.[2,+∞) | C.(4,+∞) | D.[4,+∞) |
正实数 满足
满足 设
设 ,则:
,则:
| A.p>2012 | B.p=2012 | C.p<2012 | D.p≤2012 |
若函数 在
在 处有最小值,则
处有最小值,则 ( )
( )
A. | B. | C.4 | D.3 |
 均为正实数,则
均为正实数,则 的最大值是 _____ .
的最大值是 _____ .