题目内容
已知函数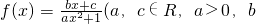 是自然数)是奇函数,f(x)有最大值
是自然数)是奇函数,f(x)有最大值 ,且
,且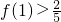 ,试求函数f(x)的解析式.
,试求函数f(x)的解析式.
解:由f(x)为奇函数得f(-x)+f(x)=0,即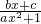 +
+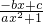 =0,
=0,
∴c=0.
又a>0,b是自然数,
∴当x<0时,f(x)<0,
当x>0时,f(x)>0,
故f(x)的最大值 必在x>0时取得;
必在x>0时取得;
当x>0时,f(x)=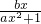 =
=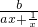 ≤
≤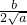 ,
,
当且仅当ax= ,即x=
,即x= 时取得
时取得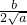 =
= ,即a=b2,
,即a=b2,
又f(1)> ,
,
∴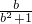 >
> ,
,
∴2b2-5b+2<0,即(2b-1)(b-2)<0,
∴ <b<2 又a>0,b是自然数可得a=b=1,
<b<2 又a>0,b是自然数可得a=b=1,
∴f(x)= .
.
分析:由f(x)为奇函数可知f(-x)+f(x)=0,求得c=0; 依题意可知f(x)的最大值 必在x>0时取得,利用基本不等式可求得f(x)≤
必在x>0时取得,利用基本不等式可求得f(x)≤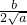 =
= ,于是a=b2,最后由f(1)>
,于是a=b2,最后由f(1)> ,即可求得
,即可求得 <b<2 又a>0,b是自然数可得a=b=1.
<b<2 又a>0,b是自然数可得a=b=1.
点评:本题考查函数奇偶性的性质,考查基本不等式的应用,由基本不等式结合题意得到a=b2是关键,考查分析、转化与运算能力,属于中档题.
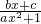 +
+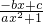 =0,
=0,∴c=0.
又a>0,b是自然数,
∴当x<0时,f(x)<0,
当x>0时,f(x)>0,
故f(x)的最大值
 必在x>0时取得;
必在x>0时取得;当x>0时,f(x)=
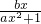 =
=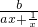 ≤
≤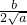 ,
,当且仅当ax=
 ,即x=
,即x= 时取得
时取得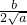 =
= ,即a=b2,
,即a=b2,又f(1)>
 ,
,∴
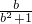 >
> ,
,∴2b2-5b+2<0,即(2b-1)(b-2)<0,
∴
 <b<2 又a>0,b是自然数可得a=b=1,
<b<2 又a>0,b是自然数可得a=b=1,∴f(x)=
 .
.分析:由f(x)为奇函数可知f(-x)+f(x)=0,求得c=0; 依题意可知f(x)的最大值
 必在x>0时取得,利用基本不等式可求得f(x)≤
必在x>0时取得,利用基本不等式可求得f(x)≤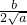 =
= ,于是a=b2,最后由f(1)>
,于是a=b2,最后由f(1)> ,即可求得
,即可求得 <b<2 又a>0,b是自然数可得a=b=1.
<b<2 又a>0,b是自然数可得a=b=1.点评:本题考查函数奇偶性的性质,考查基本不等式的应用,由基本不等式结合题意得到a=b2是关键,考查分析、转化与运算能力,属于中档题.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
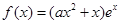 ,其中e是自然数的底数,
,其中e是自然数的底数,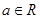 .
.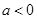 时,解不等式
时,解不等式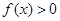 ;
; 时,求整数k的所有值,使方程
时,求整数k的所有值,使方程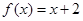 在[k,k+1]上有解;
在[k,k+1]上有解;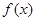 在[-1,1]上是单调增函数,求
在[-1,1]上是单调增函数,求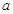 的取值范围.
的取值范围.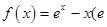 是自然数对数的底数)
是自然数对数的底数)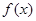 的最小值;
的最小值;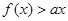 的解集为P,若
的解集为P,若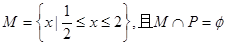 ,求实数
,求实数 的取值范围。
的取值范围。