题目内容
求过点A(0,6)且与圆C:x2+y2+10x+10y=0切于原点的圆的方程.
活动:学生思考交流,回顾圆的方程的求法,教师引导学生注意题目的条件,灵活处理,如图3.所求圆经过原点和A(0,6),且圆心应在已知圆的圆心与原点的连线上.根据这三个条件可确定圆的方程.
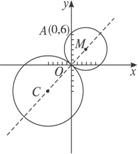
图3
解:将圆C化为标准方程,得(x+5)2+(y+5)2=50,
则圆心为C(-5,-5),半径为
.所以经过此圆心和原点的直线方程为x-y=0.
设所求圆的方程为(x-a)2+(y-b)2=r2.
由题意,知O(0,0),A(0,6)在此圆上,且圆心M(a,b)在直线x-y=0上,则有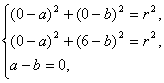
解得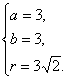
于是所求圆的方程是(x-3)2+(y-3)2=18.
点评:求圆的方程,一般可从圆的标准方程和一般方程入手,至于选择哪一种方程形式更恰当,要根据题目的条件而定,总之要让所选择的方程形式使解题过程简单.
练习册系列答案
相关题目