题目内容
设数列{an}的前n项和为Sn,对一切n∈N*,点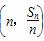 都在函数f(x)=x+
都在函数f(x)=x+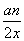 的图象上.
的图象上.
(1)求a1、a2、a3的值,猜想an的表达式,并用数学归纳法证明;
(2)将数列{an}依次按1项、2项、3项、4项循环地分为(a1),(a2,a3),(a4,a5,a6),(a7,a8,a9,a10);(a11),(a12,a13),(a14,a15,a16),(a17,a18,a19,a20);(a21),…,分别计算各个括号内各数之和,设由这些和按原来括号的前后顺序构成的数列为{bn},求b5+b100的值.
(1)∵点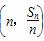 在函数f(x)=x+
在函数f(x)=x+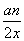 的图象上,
的图象上,
∴ =n+
=n+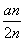 ,∴Sn=n2+
,∴Sn=n2+ an.
an.
令n=1得,a1=1+ a1,∴a1=2;
a1,∴a1=2;
令n=2得,a1+a2=4+ a2,∴a2=4;
a2,∴a2=4;
令n=3得,a1+a2+a3=9+ a3,∴a3=6.
a3,∴a3=6.
由此猜想:an=2n.
用数学归纳法证明如下:
①当n=1时,由上面的求解知,猜想成立.
②假设n=k(k≥1)时猜想成立,即ak=2k成立,
则当n=k+1时,注意到Sn=n2+ an(n∈N*),
an(n∈N*),
故Sk+1=(k+1)2+ ak+1,Sk=k2+
ak+1,Sk=k2+ ak.
ak.
两式相减得,ak+1=2k+1+ ak+1-
ak+1- ak,所以ak+1=4k+2-ak.
ak,所以ak+1=4k+2-ak.
由归纳假设得,ak=2k,
故ak+1=4k+2-ak=4k+2-2k=2(k+1).
这说明n=k+1时,猜想也成立.
由①②知,对一切n∈N*,an=2n成立.
(2)因为an=2n(n∈N*),所以数列{an}依次按1项、2项、3项、4项循环地分为(2),(4,6),(8,10,12),(14,16,18,20);(22),(24,26),(28,30,32),(34,36,38,40);(42),….每一次循环记为一组.由于每一个循环含有4个括号,故b100是第25组中第4个括号内各数之和.由分组规律知,各组第4个括号中所有第1个数组成的数列是等差数列,且公差为20.同理,由各组第4个括号中所有第2个数、所有第3个数、所有第4个数分别组成的数列也都是等差数列,且公差均为20.故各组第4个括号中各数之和构成等差数列,且公差为80.注意到第一组中第4个括号内各数之和是68,
所以b100=68+24×80=1988,
又b5=22,所以b5+b100=2010.
.

 名校课堂系列答案
名校课堂系列答案 =ad-bc,若
=ad-bc,若 =1-2i,设i为虚数单位,则复数z=________.
=1-2i,设i为虚数单位,则复数z=________. ,所以过P的切线的斜率k=
,所以过P的切线的斜率k= .类比上述方法求出双曲线x2-
.类比上述方法求出双曲线x2-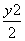 =1在P(
=1在P(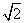 ,
, ≤n+1(n∈N*),某人的证明过程如下:
≤n+1(n∈N*),某人的证明过程如下: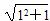 ≤1+1,不等式成立.
≤1+1,不等式成立. 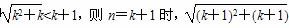 =
=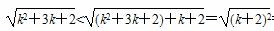 =(k+1)+1.
=(k+1)+1.