题目内容
直线
将圆
分割成的两段圆孤长之比为( )
A． | B． | C． | D． |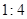
B
解析试题分析：圆心
到直线的距离为
直线被圆所截得的弦长为
,所以圆心角为
,故分割成的两段圆孤长之比为.
考点：直线与圆的位置关系,弦长公式.
练习册系列答案
名校课堂系列答案
相关题目
圆
上的点到点
的距离的最小值是（ ）
| A．1 | B．4 | C．5 | D．6 |
已知圆
，定点
，点
为圆
上的动点，点
在
上，点
在线段
上，且满足
，则点的轨迹方程是（ ）
A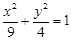． | B． | C． | D． |
直线
与圆
相交所得的弦的长为（ ）
A． | B． | C． | D． |
已知直线
（
）经过圆
的圆心，则
的最小值是( )
| A．9 | B．8 | C．4 | D．2 |
一动圆与圆
外切，同时与圆
内切，则动圆的圆心在（ ）
| A．一个椭圆上 | B．一条抛物线上 |
| C．双曲线的一支上 | D．一个圆上 |
点P(4,-2)与圆x2+y2=4上任一点连线的中点的轨迹方程是( )
| A．(x-2)2+(y+1)2=1 | B．(x-2)2+(y+1)2=4 |
| C．(x+4)2+(y-2)2=4 | D．(x+2)2+(y-1)2=1 |
圆(x＋2)2＋y2＝4与圆(x－2)2＋(y－1)2＝9的位置关系为( )．
| A．内切 | B．相交 | C．外切 | D．相离 |
直线l：y＝k(x－2)＋2与圆C：x2＋y2－2x－2y＝0相切，则直线l的斜率为( )．
| A．－1 | B．－2 | C．1 | D．2 |