题目内容
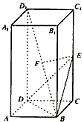
矩形ABCD与矩形ADEF所在的平面互相垂直,将△DEF沿FD翻折,翻折后的点E恰与BC上的点P重合.设AB=1,FA=x(x>1),AD=y,则当x=______时,y有最小值.
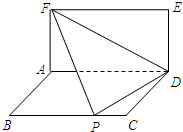

∵形ABCD与矩形ADEF所在的平面互相垂直,
AB=1,FA=x(x>1),AD=y,
∴FE=FP=AD=BC=y,AB=DC=1,FA=DE=DP=x
在Rt△DCP中,PC=
在Rt△FAP中,AP=
在Rt△ABP中,BP=
∵BC=BP+PC=
+
=y
整理得y2=
=
,令t=
则y2=
,
则当t=
,即x=
时,y取最小值.
故答案为:
AB=1,FA=x(x>1),AD=y,
∴FE=FP=AD=BC=y,AB=DC=1,FA=DE=DP=x
在Rt△DCP中,PC=
| x2-1 |
在Rt△FAP中,AP=
| y2-x2 |
在Rt△ABP中,BP=
| y2-x2-1 |
∵BC=BP+PC=
| y2-x2-1 |
| x2-1 |
整理得y2=
| x4 |
| x2-1 |
| 1 | ||||
|
| 1 |
| x2 |
则y2=
| 1 |
| -t2+t |
则当t=
| 1 |
| 2 |
| 2 |
故答案为:
| 2 |

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
 是
是 上的直径,点
上的直径,点 是
是 垂直于
垂直于 ,
, 分别是
分别是 ,
, 与平面
与平面 的位置关系,并说明理由.
的位置关系,并说明理由.
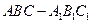 中,
中,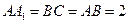 ,
,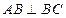 ,求二面角
,求二面角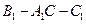 的大小.
的大小.