题目内容
双曲线(1)若![]() =5
=5![]() ,求直线l的斜率;
,求直线l的斜率;
(2)证明M、N两点的纵坐标之积为-![]() a2.
a2.
(1)解:设P(x1,y1),Q(x2,y2),因为双曲线的离心率为![]() ,?
,?
所以c=![]() a,b=
a,b=![]() a,双曲线方程为2x2-y2=
a,双曲线方程为2x2-y2=
因为![]() =5
=5![]() ,所以x2=
,所以x2=![]() c. ?
c. ?
因为直线l:y=k(x-c),?
所以y2=-![]() . ?
. ?
点Q是双曲线上一点,所以2(![]() )2-(-
)2-(-![]() )2=
)2=
整理,得![]() e2-
e2-![]() e2k2=2,解得k=±
e2k2=2,解得k=±![]() . ?
. ?
(2)证明:设P(x1,y1),Q(x2,y2),?
由已知AP:y=![]() (x+a),AQ:y=
(x+a),AQ:y=![]() (x+a),?
(x+a),?
所以ym=![]() (
(![]() +a),yn==
+a),yn==![]() (
(![]() +a). ?
+a). ?
所以ymyn=![]() ·
·![]() (
(![]() +a)2=
+a)2=![]() (
(![]() +a)2.?
+a)2.?
由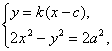 得(2-k2)x2+2k2cx-k
得(2-k2)x2+2k2cx-k
所以x1+x2=![]() ,x1x2=
,x1x2=![]() ,?
,?
y1y2=k2(x1-c)(x2-c)=k2[x1x2-c(x1+x2)+c2]=k2![]() , ?
, ?
x1x2+a(x1+x2)+a2=k2![]() . ?
. ?
所以ymyn=![]() ·
·![]() =-
=-![]() a2.
a2.

 阅读快车系列答案
阅读快车系列答案

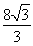

 -
-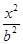 =1(a>0, b>0)有相同的焦点F,点B是两曲线的一
=1(a>0, b>0)有相同的焦点F,点B是两曲线的一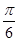 ,
,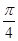 ) B.(
) B.(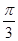 ) C.(
) C.( ,
,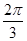 ) D.(
) D.(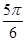 ,π)
,π)