题目内容
在数列![]() 中,已知
中,已知![]() ,
,![]() ,
,![]() .(1)证明数列
.(1)证明数列![]() 为等比数列,并求数列
为等比数列,并求数列![]() 的通项公式;
的通项公式;
(2)求证:![]() ,
,![]() .
.
(1)数列![]() 的通项公式是
的通项公式是![]()
(2)见解析
解析:
(1)注意到![]() ,所以原式整理得:
,所以原式整理得:![]()
由![]() ,
,![]() 得对
得对![]() ,
,![]() .从而由
.从而由![]() ,两边取倒数得:
,两边取倒数得:![]() ,即
,即![]()
![]() ,
,![]()
![]() 数列
数列 是首项为
是首项为![]() ,公比为
,公比为![]() 的等比数列
的等比数列 ![]()
![]() .
.![]() 故数列
故数列![]() 的通项公式是
的通项公式是![]() . ……4分
. ……4分
(2)证法1:![]() ,
,![]() 当
当![]() 时,
时,
![]()
![]() ……8分
……8分
![]()
![]()
![]() +
+![]()
![]()
![]()
![]()
![]() .…………………………………………………………12分
.…………………………………………………………12分
证法2:![]() ,
,![]() 当
当![]() 时,
时,
![]() ………………8分
………………8分
![]()
![]()
![]()
![]()
![]()
![]() .………………………………………………………………………………12分
.………………………………………………………………………………12分

练习册系列答案
相关题目
 是等差数列,
是等差数列, 是各项都为正数的等比数列,且
是各项都为正数的等比数列,且 .
.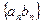 的前
的前 项和
项和 中,已知:
中,已知: .
.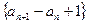 是
是 等比数列.
等比数列. .
.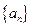 中,已知
中,已知
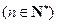 .
. 项和
项和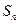 .
. 中,已知
中,已知 且
且 。
。 证明:数列
证明:数列 是等差数列,并求数列
是等差数列,并求数列 求
求 的值。
的值。 中,已知
中,已知 ,
, .
.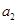 、
、 并判断
并判断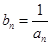 ,求证:
,求证: 为等比数列;
为等比数列;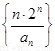 的前n项和
的前n项和 .
.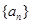 中,已知
中,已知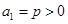 ,且
,且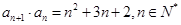 .
.