题目内容
函数y=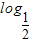
（x2-5x+6）的单调减区间为（ ）A．（
，+∞）B．（3，+∞）
C．（-∞，
）D．（-∞，2）
【答案】分析：先求得函数y=
（x2-5x+6）的定义域为（-∞，2）∪（3，+∞），本题即求函数t在（-∞，2）∪（3，+∞）上的增区间．结合二次函数的性质可得函数t在（-∞，2）∪（3，+∞）上的增区间．
解答：解：令t=x2-5x+6=（x-2）（x-3）＞0，可得 x＜2，或 x＞3，故函数y=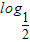
（x2-5x+6）的定义域为（-∞，2）∪（3，+∞）．
本题即求函数t在（-∞，2）∪（3，+∞）上的增区间．
结合二次函数的性质可得，函数t在（-∞，2）∪（3，+∞）上的增区间为 （3，+∞），
故选B．
点评：本题主要考查复合函数的单调性，体现了转化的数学思想，属于中档题．
（x2-5x+6）的定义域为（-∞，2）∪（3，+∞），本题即求函数t在（-∞，2）∪（3，+∞）上的增区间．结合二次函数的性质可得函数t在（-∞，2）∪（3，+∞）上的增区间．解答：解：令t=x2-5x+6=（x-2）（x-3）＞0，可得 x＜2，或 x＞3，故函数y=
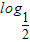（x2-5x+6）的定义域为（-∞，2）∪（3，+∞）．本题即求函数t在（-∞，2）∪（3，+∞）上的增区间．
结合二次函数的性质可得，函数t在（-∞，2）∪（3，+∞）上的增区间为 （3，+∞），
故选B．
点评：本题主要考查复合函数的单调性，体现了转化的数学思想，属于中档题．
练习册系列答案
相关题目