题目内容
己知,其中常数.
(1)当时,求函数的极值;
(2)若函数有两个零点,求证:;
(3 )求证:.
)求证:.
解:函数的定义域为,
(1)当时,,, …………1分
而 在上单调递增,又,
在上单调递增,又,
当时,,则在上单调递减;
当时,,则在上单调递增, …………2分
所以有极小值,没有极大值. …………3分
(2)先证明:当恒成立时,有 成立.
若,则显然成立;…………4分
若,由得,
令,则,…………5分
令,由 得
得
在上单调递增,
又因为,所以在上 为负,在上为正,
为负,在上为正,
因此在上递减,在上递增,所以,
从而.…………6分
因而函数若有两个零点,则,
所以,
由得,则
,
所以在上单调递增,
所以,
所以在上单调递增,
所以,
则,所以,…………8分
由得,
则,所以,
综上得. …………9分
(3)由(2)知当时,恒成立,所以,
即,设,则,
当时, ,所以在上单调递增;
当时,,所以在上单调递增, …………10分
所以的最大值为,即,因而,…………11分
所以,即. …………12分
考点:1.用导数研究函数的最值和极值;2.零点存在性定理;3.构造函数证明不等式.

练习册系列答案
 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目
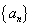 满足
满足 ,则其前
,则其前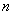 项和
项和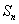 = .
= . 、
、 是两条不同的直线,
是两条不同的直线, 、
、 是两个不同的平面,下列命题正确的是( )
是两个不同的平面,下列命题正确的是( ) ,
, ,则
,则 B.若
B.若 ,则
,则
 ,
, D.若
D.若 ,
,
 中,
中, ,点
,点 在
在 上,
上, ,
, = .
= .

 为椭圆
为椭圆 上两点.点
上两点.点 关于
关于 轴对称点为
轴对称点为 (异于点
(异于点 ).若直线
).若直线 分别与
分别与 , 则
, 则 =( )
=( ) D.2
D.2 ,且
,且 ,则
,则 的最小值是( )
的最小值是( ) B.
B. C.
C. D.
D.
 是首项为
是首项为 ,公比
,公比 的等比数列,
的等比数列,



 ,数列
,数列 满足
满足 .
. 是等差数列;
是等差数列;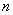 项和
项和 ;
; 对一切正整数
对一切正整数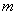 的取值范围.
的取值范围.