题目内容
当n∈N*时，Sn=1-
+
-
+…+
-
，Tn=
+
+
+…+
．
（Ⅰ）求S1，S2，T1，T2；
（Ⅱ）猜想Sn与Tn的关系，并用数学归纳法证明．
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 2n-1 |
| 1 |
| 2n |
| 1 |
| n+1 |
| 1 |
| n+2 |
| 1 |
| n+3 |
| 1 |
| 2n |
（Ⅰ）求S1，S2，T1，T2；
（Ⅱ）猜想Sn与Tn的关系，并用数学归纳法证明．
（Ⅰ）∵当n∈N*时，Sn=1-
+
-
+…+
-
，Tn=
+
+
+…+
．
∴S1=1-
=
，S2=1-
+
-
=
，T1=
=
，T2=
+
=
（2分）
（Ⅱ）猜想：Sn=Tn（n∈N*），即：
1-
+
-
+…+
-
=
+
+
+…+
（n∈N*）（5分）
下面用数学归纳法证明：
①当n=1时，已证S1=T1（6分）
②假设n=k时，Sk=Tk（k≥1，k∈N*），
即：1-
+
-
+…+
-
=
+
+
+…+
（8分）
则：Sk+1=Sk+
-
=Tk+
-
（10分）
=
+
+
+…+
+
-
（11分）
=
+
+…+
+
+（
-
）
=
+
+…+
+
=Tk+1，
由①，②可知，对任意n∈N*，Sn=Tn都成立．（14分）
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 2n-1 |
| 1 |
| 2n |
| 1 |
| n+1 |
| 1 |
| n+2 |
| 1 |
| n+3 |
| 1 |
| 2n |
∴S1=1-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 7 |
| 12 |
| 1 |
| 1+1 |
| 1 |
| 2 |
| 1 |
| 2+1 |
| 1 |
| 2+2 |
| 7 |
| 12 |
（Ⅱ）猜想：Sn=Tn（n∈N*），即：
1-
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 2n-1 |
| 1 |
| 2n |
| 1 |
| n+1 |
| 1 |
| n+2 |
| 1 |
| n+3 |
| 1 |
| 2n |
（n∈N*）（5分）
下面用数学归纳法证明：
①当n=1时，已证S1=T1（6分）
②假设n=k时，Sk=Tk（k≥1，k∈N*），
即：1-
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 2k-1 |
| 1 |
| 2k |
| 1 |
| k+1 |
| 1 |
| k+2 |
| 1 |
| k+3 |
| 1 |
| 2k |
则：Sk+1=Sk+
| 1 |
| 2k+1 |
| 1 |
| 2(k+1) |
| 1 |
| 2k+1 |
| 1 |
| 2(k+1) |
=
| 1 |
| k+1 |
| 1 |
| k+2 |
| 1 |
| k+3 |
| 1 |
| 2k |
| 1 |
| 2k+1 |
| 1 |
| 2(k+1) |
=
| 1 |
| k+2 |
| 1 |
| k+3 |
| 1 |
| 2k |
| 1 |
| 2k+1 |
| 1 |
| k+1 |
| 1 |
| 2(k+1) |
=
| 1 |
| (k+1)+1 |
| 1 |
| (k+1)+2 |
| 1 |
| 2k+1 |
| 1 |
| 2(k+1) |
由①，②可知，对任意n∈N*，Sn=Tn都成立．（14分）
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
ABCD所在平面与正方形ABEF所在平面互相垂直，M为AC上一点，N为BF 上一点，且
有，设
；
；
为何值时，
取最小值？并求出这个最小值.
满足
, 
，
．
是等比数列；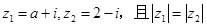 
，则实数a的值为
或0