题目内容
四棱锥P-ABCD的顶点P在底面ABCD中的投影恰好是A,其三视图如图,则四棱锥P-ABCD的表面积为.( )
A.(2+
 )a2
)a2B.(2-
 )a2
)a2C.2+
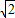 )
)D.(2-
 )π
)π
【答案】分析:由四棱锥P-ABCD的顶点P在底面ABCD中的投影恰好是A,我们易得PA是棱锥的高,由三视图我们易得底面边长,及棱锥的高均为a,由此我们易求出各棱的长,进而求出各个面的面积,进而求出四棱锥P-ABCD的表面积;
解答:解:由三视图可得,三角形ABP的面积等于三角形ADP的面积且为 a2,
a2,
三角形BPC的面积等于三角形CDP的面积且为 a2,
a2,
正方形ABCD的面积为a2,
侧面积为:S△PAB+S△PBC+S△PCD+S△PAD=2× +2×
+2× ×
× =(1+
=(1+ )a2
)a2
所以可得四棱锥P-ABCD的表面积为(2+ )a2.
)a2.
故选A;
点评:本题考查的知识点由三视图求表面积,根据三视图及已知求出棱锥各棱长的长度,进而求出各面的面积,是解答本题的关键.
解答:解:由三视图可得,三角形ABP的面积等于三角形ADP的面积且为
 a2,
a2,三角形BPC的面积等于三角形CDP的面积且为
 a2,
a2,正方形ABCD的面积为a2,
侧面积为:S△PAB+S△PBC+S△PCD+S△PAD=2×
 +2×
+2× ×
× =(1+
=(1+ )a2
)a2所以可得四棱锥P-ABCD的表面积为(2+
 )a2.
)a2.故选A;
点评:本题考查的知识点由三视图求表面积,根据三视图及已知求出棱锥各棱长的长度,进而求出各面的面积,是解答本题的关键.

练习册系列答案
相关题目
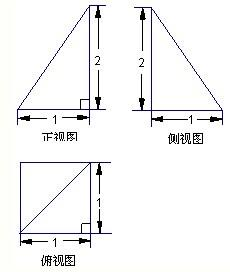 已知四棱锥P-ABCD的三视图如图所示,则这个四棱锥的体积为( )
已知四棱锥P-ABCD的三视图如图所示,则这个四棱锥的体积为( )A、
| ||
| B、1 | ||
C、
| ||
D、
|
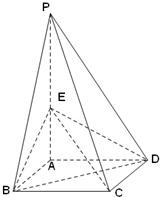 如图,四棱锥P-ABCD的底面是边长为1的正方形,侧棱PA⊥底面ABCD,且PA=2,E是PA的中点.
如图,四棱锥P-ABCD的底面是边长为1的正方形,侧棱PA⊥底面ABCD,且PA=2,E是PA的中点. 如图所示,四棱锥P-ABCD的底面是边长为a的正方形,侧棱PA⊥底面ABCD,侧面PBC内有BE⊥PC于E,且BE=
如图所示,四棱锥P-ABCD的底面是边长为a的正方形,侧棱PA⊥底面ABCD,侧面PBC内有BE⊥PC于E,且BE= 如图,ABCD是正方形,O是该正方形的中心,P是平面ABCD外一点,PO⊥底面ABCD,E是PC的中点.求证:
如图,ABCD是正方形,O是该正方形的中心,P是平面ABCD外一点,PO⊥底面ABCD,E是PC的中点.求证: