题目内容
下列函数中,最小值为2的是________
①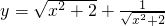 ②
②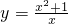 ③
③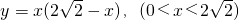 ④
④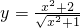 .
.
④
分析:利用不等式的性质与基本不等式可逐个判断,注意检验基本不等式成立的条件.
解答:对于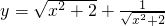 ,由于
,由于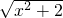 和
和 不相等,故y>2,故排除①.
不相等,故y>2,故排除①.
对于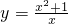 =
= ,当x≥0时,ymin=2,故排除②.
,当x≥0时,ymin=2,故排除②.
对于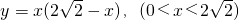 ,当x趋于0时,函数y的值趋于0,故最小值不是2.
,当x趋于0时,函数y的值趋于0,故最小值不是2.
对于 ≥2(当且仅当x=0时取“=”),故④正确.
≥2(当且仅当x=0时取“=”),故④正确.
故答案为 ④.
点评:本题考查基本不等式,考查学生灵活的解决数学问题的方法,如特值法,排除法,分析计算法等,属于基础题.
分析:利用不等式的性质与基本不等式可逐个判断,注意检验基本不等式成立的条件.
解答:对于
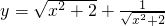 ,由于
,由于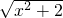 和
和 不相等,故y>2,故排除①.
不相等,故y>2,故排除①.对于
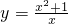 =
= ,当x≥0时,ymin=2,故排除②.
,当x≥0时,ymin=2,故排除②.对于
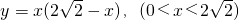 ,当x趋于0时,函数y的值趋于0,故最小值不是2.
,当x趋于0时,函数y的值趋于0,故最小值不是2.对于
 ≥2(当且仅当x=0时取“=”),故④正确.
≥2(当且仅当x=0时取“=”),故④正确.故答案为 ④.
点评:本题考查基本不等式,考查学生灵活的解决数学问题的方法,如特值法,排除法,分析计算法等,属于基础题.

练习册系列答案
相关题目
下列函数中,最小值为2的是( )
A、y=
| ||||
B、y=lgx+
| ||||
| C、y=3x+3-x,x∈R | ||||
D、y=sin x+
|