题目内容
设函数f(x)=sinx-cosx+x+1,0<x<2π,求函数f(x)的单调区间与极值.
由f(x)=sinx-cosx+x+1,0<x<2π,知f'(x)=1+
sin(x+
).
令f'(x)=0,从而可得sin(x+
)=-
,得x=π,或x=
,
当x变化时,f'(x),f(x)变化情况如下表:
因此,由上表知f(x)的单调递增区间是(0,π)与(
,2π),
单调递减区间是(π,
),极小值为f(
)=
,极大值为f(π)=π+2
| 2 |
| π |
| 4 |
令f'(x)=0,从而可得sin(x+
| π |
| 4 |
| ||
| 2 |
| 3π |
| 2 |
当x变化时,f'(x),f(x)变化情况如下表:
| x | (0,π) | π | (π,
|
|
(
| ||||||
| f'(x) | + | 0 | - | 0 | + | ||||||
| f(x) | 单调递增↑ | π+2 | 单调递减↓ |
|
单调递增↑ |
| 3π |
| 2 |
单调递减区间是(π,
| 3π |
| 2 |
| 3π |
| 2 |
| 3π |
| 2 |

练习册系列答案
相关题目
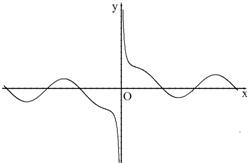 如图是函数Q(x)的图象的一部分,设函数f(x)=sinx,g ( x )=
如图是函数Q(x)的图象的一部分,设函数f(x)=sinx,g ( x )=| 1 |
| x |
A、
| ||
| B、f(x)g(x) | ||
| C、f(x)-g(x) | ||
| D、f(x)+g(x) |
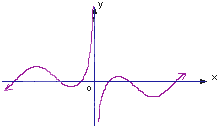 设函数f(x)=sinx,g(x)=
设函数f(x)=sinx,g(x)=