题目内容
已知函数: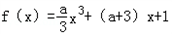 .
.
(1)当a=﹣3时,求过点(1,0)曲线y=f(x)的切线方程;
(2)求函数y=f(x)的单调区间;
(3)函数是否存在极值?若有,则求出极值点;若没有,则说明理由.
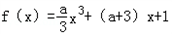 .
.(1)当a=﹣3时,求过点(1,0)曲线y=f(x)的切线方程;
(2)求函数y=f(x)的单调区间;
(3)函数是否存在极值?若有,则求出极值点;若没有,则说明理由.
解:(1)当a=﹣3时,f(x)=﹣x3+1对函数求导可得,f'(x)=﹣3x2
由导数的几何意义可得,曲线在(1,0)处的切线的斜率k=f'(1)=﹣3
∴过点(1,0)曲线y=f(x)的切线方程为y=﹣3(x﹣1)
即3x+y﹣3=0
(2)对函数求导可得,f'(x)=ax2+(a+3),
①当a≥0时,f'(x)>0,f(x)在(﹣∞,+∞)单调递增
②当a≤﹣3时,f'(x)≤0,f(x)在(﹣∞,+∞)单调递减
③当﹣3<a<0,由f'(x)>0,可得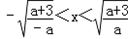 ,
,
即f(x)在(﹣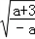 ,+
,+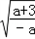 )单调递增;
)单调递增;
f'(x)≤0,f(x)在(﹣∞,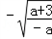 ],[
],[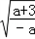 ,+∞)单调递减
,+∞)单调递减
(3)由(2)得,当﹣3<a<0,函数在x=﹣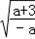 存在极小值,在x=
存在极小值,在x=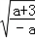 存在极大值
存在极大值
由导数的几何意义可得,曲线在(1,0)处的切线的斜率k=f'(1)=﹣3
∴过点(1,0)曲线y=f(x)的切线方程为y=﹣3(x﹣1)
即3x+y﹣3=0
(2)对函数求导可得,f'(x)=ax2+(a+3),
①当a≥0时,f'(x)>0,f(x)在(﹣∞,+∞)单调递增
②当a≤﹣3时,f'(x)≤0,f(x)在(﹣∞,+∞)单调递减
③当﹣3<a<0,由f'(x)>0,可得
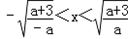 ,
,即f(x)在(﹣
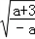 ,+
,+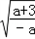 )单调递增;
)单调递增;f'(x)≤0,f(x)在(﹣∞,
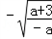 ],[
],[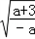 ,+∞)单调递减
,+∞)单调递减(3)由(2)得,当﹣3<a<0,函数在x=﹣
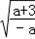 存在极小值,在x=
存在极小值,在x=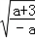 存在极大值
存在极大值
练习册系列答案
 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
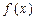 ,如果满足:对任意
,如果满足:对任意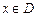 ,存在常数
,存在常数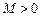 ,都有
,都有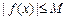 成立,则称
成立,则称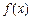 是D上的有界函数,其中M称为函数
是D上的有界函数,其中M称为函数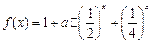 ;
;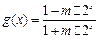 .
.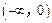 上的值域,并判断函数
上的值域,并判断函数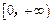 上是以3为上界的
上是以3为上界的 有界函数,求实数a的取值范围;
有界函数,求实数a的取值范围;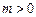 ,函
,函 数
数 在
在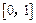 上的上界是
上的上界是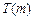 ,求
,求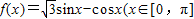 ),
),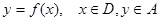 ;
;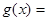
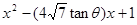 ,
,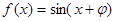 为偶函数时,求
为偶函数时,求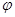 的值。
的值。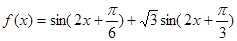 时,
时,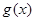 在
在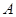 上是单调递增函数,求
上是单调递增函数,求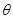 的取值范围。
的取值范围。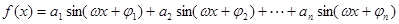 时,(其中
时,(其中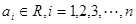 ,
,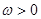 ),若
),若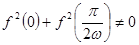 ,且函数
,且函数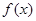 的图像关于点
的图像关于点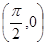 对称,在
对称,在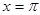 处取得最小值,试探讨
处取得最小值,试探讨 应该满足的条件。
应该满足的条件。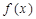 ,如果满足:对任意
,如果满足:对任意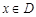 ,存在常数
,存在常数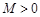 ,都有
,都有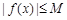 成立,则称
成立,则称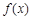 是D上的有界函数,其中M称为函数
是D上的有界函数,其中M称为函数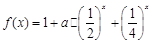 ;
;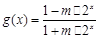 .
.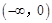 上的值域,并判断函数
上的值域,并判断函数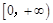 上是以3为上界的有界函数,求实数a的取值范围;
上是以3为上界的有界函数,求实数a的取值范围;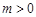 ,函数
,函数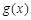 在
在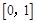 上的上界是
上的上界是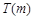 ,求
,求 ,如果满足:对任意
,如果满足:对任意 ,存在常数
,存在常数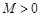 ,都有
,都有 成立,则称
成立,则称 是D上的有界函数,其中M称为函数
是D上的有界函数,其中M称为函数 ;
; .
. 上的值域,并判断函数
上的值域,并判断函数 上是以3为上界的有界函数,求实数a的取值范围;
上是以3为上界的有界函数,求实数a的取值范围; ,函数
,函数 在
在 上的上界是
上的上界是 ,求
,求